
【题目】如图1是一个长为2a,宽为2b的 长方形,沿图中虚线剪开分成四块小长方形,然后按如图2的形状拼成一个正方形。
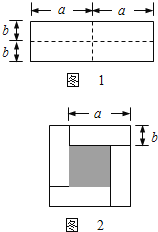
(1)图2的阴影部分的正方形的边长是 .
(2)用两种不同的方法求图中阴影部分的面积.
(方法1)S阴影= ;
(方法2)S阴影= ;
(3)观察如图2,写出(a+b)2、(a-b)2,ab三个代数式之间的等量关系.
(4)根据(3)题中的等量关系,解决问题:若x+y=10,xy=16,求x-y的值。
【答案】(1)a-b;(2)(a+b)2-4ab,(a-b)2;(3)(a+b)2-4ab=(a-b)2;(4)±6
【解析】
(1)观察图意直接得出正方形的边长是a-b;(2)利用大正方形的面积减去4个小长方形的面积,或者直接利用(1)的条件求出小正方形的面积;(3)把(2)中的两个代数式联立即可;(4)类比(3)求出(x-y)2,再开方即可.
(1)观察图意直接得出正方形的边长是a-b;
(2)利用大正方形的面积减去4个小长方形的面积则S阴影=(a+b)2-4ab,
直接利用(1)的条件求出小正方形的面积则S阴影=(a-b)2;
(3)由S阴影的两种写法得(a+b)2-4ab=(a-b)2;
(4)由(3)可得(x-y)2=(x+y)2-4xy,
则(x-y)2=102-4×16=36,
∴x-y=±6,


 名题训练系列答案
名题训练系列答案 期末集结号系列答案
期末集结号系列答案科目:初中数学 来源: 题型:
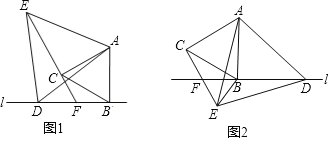
【题目】已知线段AB⊥直线l于点B,点D在直线l上,分别以AB,AD为边作等边三角形ABC和等边三角形ADE,直线CE交直线l于点F
(1)当点F在线段BD上时,如图1,线段DF,CE,CF之间的数量关系是 ;
(2)当点F在线段DB的延长线上时,如图2.
①(1)中的数量关系是否仍然成立?若成立,请写出证明过程;若不成立,请重新写出正确的结论,并写出证明过程;
②若等边△ABC和等边△ADE的边长分别是![]() 和
和![]() ,DF=3,求BE的长.
,DF=3,求BE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】观察图形,解答问题:

(1)按下表已填写的形式填写表中的空格:
图① | 图② | 图③ | |
三个角上三个数的积 | 1×(﹣1)×2=﹣2 | (﹣3)×(﹣4)×(﹣5)=﹣60 |
|
三个角上三个数的和 | 1+(﹣1)+2=2 | (﹣3)+(﹣4)+(﹣5)=﹣12 |
|
积与和的商 | (﹣2)÷2=﹣1 |
|
|
(2)请用你发现的规律求出图④中的数x.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)如图,在四边形 ![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,求证:
,求证:![]() .
.

(2)如图,在离水面高度为 ![]() 米的岸上,有人用绳子拉船靠岸,开始时绳子
米的岸上,有人用绳子拉船靠岸,开始时绳子 ![]() 的长为
的长为 ![]() 米,此人以
米,此人以 ![]() 米每秒的速度收绳,
米每秒的速度收绳,![]() 秒后船移动到点
秒后船移动到点 ![]() 的位置,问船向岸边移动了多少米?(假设绳子是直的,结果保留根号).
的位置,问船向岸边移动了多少米?(假设绳子是直的,结果保留根号).

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AD为∠BAC的平分线,DE⊥AB于E,DF⊥AC于F,
(1)证明AE=AF;
(2)若△ABC面积是36cm2,AB=10cm,AC=8cm,求DE的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
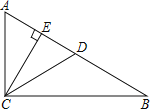
【题目】在直角三角形ABC中,∠ACB=90°,D、E是边AB上两点,且CE所在直线垂直平分线段AD,CD平分∠BCE,BC=2![]() ,则AB=_____.
,则AB=_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】学校准备购进一批甲、乙两种办公桌若干张,并且每买1张办公桌必须买2把椅子,椅子每把100元,若学校购进20张甲种办公桌和15张乙种办公桌共花费24000元;购买10张甲种办公桌比购买5张乙种办公桌多花费2000元.
(1)求甲、乙两种办公桌每张各多少元?
(2)若学校购买甲乙两种办公桌共40张,且甲种办公桌数量不多于乙种办公桌数量的3倍,请你给出一种费用最少的方案,并求出该方案所需费用.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(问题情境)学习《探索全等三角形条件》后,老师提出了如下问题:如图①,△ABC中,若AB=12,AC=8,求BC边上的中线AD的取值范围。同学通过合作交流,得到了如下的解决方法:延长AD到E,使DE=AD,连接BE.根据SAS可证得到△ADC≌△EDB,从而根据“三角形的三边关系”可求得AD的取值范围是 。解后反思:题目中出现“中点”“中线”等条件,可考虑延长中线构造全等三角形,把分散的已知条件和所求证的结论集合到同一个三角形中.
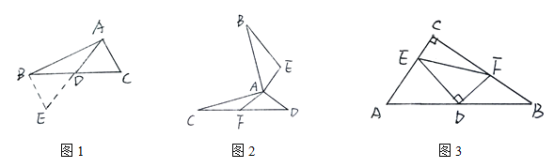
(直接运用)如图②,AB⊥AC,AD⊥AE,AB=AC,AD=AE,AF是ACD的边CD上中线.求证:BE=2AF.
(灵活运用)如图③,在△ABC中,∠C=90°,D为AB的中点,DE⊥DF,DE交AC于点E,DF交AB于点F,连接EF,试判断以线段AE、BF、EF为边的三角形形状,并证明你的结论.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】两组邻边分别相等的四边形我们称它为筝形,如图,在筝形ABCD中,AB=AD,BC=DC,AC,BD相交于点O.

(1)求证:①△ABC≌△ADC;②OB=OD,AC⊥BD;
(2)如果AC=6,BD=4,求筝形ABCD的面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com