
【题目】如图,在△ABC中,AD为∠BAC的平分线,DE⊥AB于E,DF⊥AC于F,
(1)证明AE=AF;
(2)若△ABC面积是36cm2,AB=10cm,AC=8cm,求DE的长.

【答案】(1)见解析;(2)4
【解析】
本题主要考察角平分线的性质定理和三角形面积的求法,可以根据角平分线的性质定理结合全等进行证明.
(1)证明:∵在△ABC中,AD为∠BAC的平分线,DE⊥AB,DF⊥AC,
∴∠EAD=∠FAD,∠AED=∠AFD=90°,AD=AD
∴△ADE![]() △ADF,
△ADF,
∴AE=AF;
(2)解:∵在△ABC中,AD为∠BAC的平分线,DE⊥AB,DF⊥AC,
∴DE=DF,
∵△ABC面积是36cm2,AB=10cm,AC=8cm,
∴S△ABC=S△ADB+S△ACD=![]() ABDE+
ABDE+![]() ACDF=
ACDF=![]() DE(AB+AC)=
DE(AB+AC)=![]() ×DE×(10+8)=9DE=36,
×DE×(10+8)=9DE=36,
∴DE=4(cm).


科目:初中数学 来源: 题型:
【题目】如图四边形ABCD中,AD∥BC,∠BCD=90°,∠BAD的平分线AG交BC于点G.
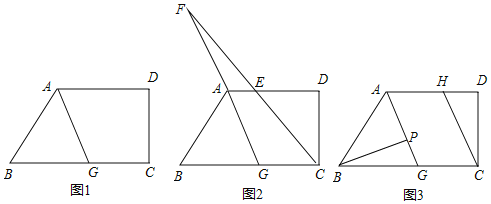
(1)求证:∠BAG=∠BGA;
(2)如图2,∠BCD的平分线CE交AD于点E,与射线GA相交于点F,∠B=50°.
①若点E在线段AD上,求∠AFC的度数;
②若点E在DA的延长线上,直接写出∠AFC的度数;
(3)如图3,点P在线段AG上,∠ABP=2∠PBG,CH∥AG,在直线AG上取一点M,使∠PBM=∠DCH,请直接写出∠ABM:∠PBM的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在⊙O中,AB为直径,D、E为圆上两点,C为圆外一点,且∠E+∠C=90°. 
(1)求证:BC为⊙O的切线.
(2)若sinA= ![]() ,BC=6,求⊙O的半径.
,BC=6,求⊙O的半径.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校为了解该校九年级学生2016年适应性考试数学成绩,现从九年级学生中随机抽取部分学生的适应性考试数学成绩,按A,B,C,D四个等级进行统计,并将统计结果绘制成如图所示不完整的统计图,请根据统计图中的信息解答下列问题:
(说明:A等级:135分﹣150分 B等级:120分﹣135分,C等级:90分﹣120分,D等级:0分﹣90分)
(1)此次抽查的学生人数为;
(2)把条形统计图和扇形统计图补充完整;
(3)若该校九年级有学生1200人,请估计在这次适应性考试中数学成绩达到120分(包含120分)以上的学生人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线y=5x+5交x轴于点A,交y轴于点C,过A,C两点的二次函数y=ax2+4x+c的图象交x轴于另一点B.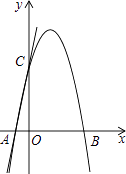
(1)求二次函数的表达式;
(2)连接BC,点N是线段BC上的动点,作ND⊥x轴交二次函数的图象于点D,求线段ND长度的最大值;
(3)若点H为二次函数y=ax2+4x+c图象的顶点,点M(4,m)是该二次函数图象上一点,在x轴、y轴上分别找点F,E,使四边形HEFM的周长最小,求出点F,E的坐标.
温馨提示:在直角坐标系中,若点P,Q的坐标分别为P(x1 , y1),Q(x2 , y2),
当PQ平行x轴时,线段PQ的长度可由公式PQ=|x1﹣x2|求出;
当PQ平行y轴时,线段PQ的长度可由公式PQ=|y1﹣y2|求出.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】若正整数k满足个位数字为1,其他数位上的数字均不为1且十位与百位上的数字相等,
我们称这样的数k为“言唯一数”,交换其首位与个位的数字得到一个新数k',并记F(k)=![]() .
.
(1)最大的四位“言唯一数”是 ,最小的三位“言唯一数”是 ;
(2)证明:对于任意的四位“言唯一数”m,m+m'能被11整除;
(3)设四位“言唯一数”n=1000x+100y+10y+1(2≤x≤9,0≤y≤9且y≠1,x、y均为整数),若F(n)仍然为“言唯一数”,求所有满足条件的四位“言唯一数”n.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com