
【题目】如图四边形ABCD中,AD∥BC,∠BCD=90°,∠BAD的平分线AG交BC于点G.
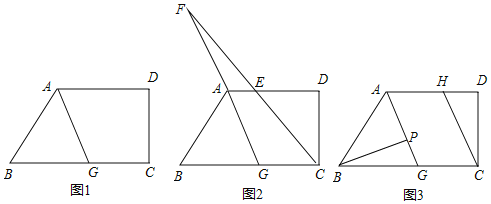
(1)求证:∠BAG=∠BGA;
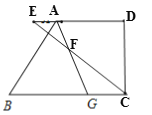
(2)如图2,∠BCD的平分线CE交AD于点E,与射线GA相交于点F,∠B=50°.
①若点E在线段AD上,求∠AFC的度数;
②若点E在DA的延长线上,直接写出∠AFC的度数;
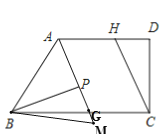
(3)如图3,点P在线段AG上,∠ABP=2∠PBG,CH∥AG,在直线AG上取一点M,使∠PBM=∠DCH,请直接写出∠ABM:∠PBM的值.
【答案】(1)证明见解析;(2)①20°;②160°;(3)![]() 或
或![]()
【解析】
(1)根据AD//BC可知∠GAD=∠BGA,由AG平分∠BAD可知∠BAG=∠GAD,即可得答案.(2)①根据CF平分∠BCD,∠BCD=90°,可求出∠GCF的度数,由AD//BC可求出∠AEF和∠DAB的度数,根据三角形外角的性质求出∠AFC的度数即可;②根据三角形外角性质求出即可;(3)根据M点在BP的上面和下面两种情况讨论,分别求出∠PBM和∠ABM的值即可.
(1)∵AD∥BC,
∴∠GAD=∠BGA,
∵AG平分∠BAD,
∴∠BAG=∠GAD,
∴∠BAG=∠BGA;
(2)①∵CF平分∠BCD,∠BCD=90°,
∴∠GCF=45°,
∵AD∥BC,∠ABC=50°,
∴∠AEF=∠GCF=45°;∠DAB=180°﹣50°=130°,
∵AG平分∠BAD,
∴∠BAG=∠GAD=65°,
∴∠AFC=65°﹣45°=20°;
②如图:
∵∠AGB=65°,∠BCF=45°,
∴∠AFC=∠CGF+∠BCF=115°+45°=160°;
(3)有两种情况:
①当M在BC的下方时,如图:∵∠ABC=50°,∠ABP=2∠PBG,
∴∠ABP=(![]() )°,∠PBG=(
)°,∠PBG=(![]() )°,
)°,
∵AG∥CH,
∴∠BCH=∠AGB=65°,∵∠BCD=90°,∴∠DCH=∠PBM=90°﹣65°=25°,
∴∠ABM=∠ABP+∠PBM=(![]() +25)°=(
+25)°=(![]() )°,
)°,
∴∠ABM:∠PBM=(![]() )°:25°=
)°:25°=![]() ;
;
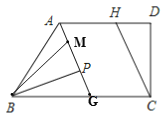
②当M在BC的上方时,如图:
同理得:∠ABM=∠ABP﹣∠PBM=(![]() ﹣25)°=(
﹣25)°=(![]() )°,
)°,
∴∠ABM:∠PBM=(![]() )°:25°=
)°:25°=![]() ;
;
综上,∠ABM:∠PBM的值是![]() 或
或![]() .
.


科目:初中数学 来源: 题型:
【题目】已知二次函数y=x2﹣(2k+1)x+k2+k(k>0)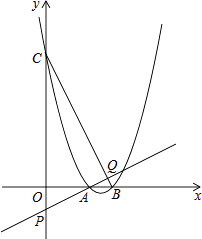
(1)当k= ![]() 时,求这个二次函数的顶点坐标;
时,求这个二次函数的顶点坐标;
(2)求证:关于x的一元次方程x2﹣(2k+1)x+k2+k=0有两个不相等的实数根;
(3)如图,该二次函数与x轴交于A、B两点(A点在B点的左侧),与y轴交于C点,P是y轴负半轴上一点,且OP=1,直线AP交BC于点Q,求证: ![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形ABCD绕点B逆时针旋转30°后得到矩形A1BC1D1 , C1D1与AD交于点M,延长DA交A1D1于F,若AB=1,BC= ![]() ,则AF的长度为( )
,则AF的长度为( ) 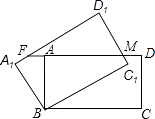
A.2﹣ ![]()
B.![]()
C.![]()
D.![]() ﹣1
﹣1
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如果一个三角形有一条边上的高等于这条边的一半,那么我们把这个三角形叫做半高三角形.已知直角三角形![]() 是半高三角形,且斜边
是半高三角形,且斜边![]() ,则它的周长等于_________.
,则它的周长等于_________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,则下列结论:①b<0,c>0;②a+b+c<0;③方程的两根之和大于0;④a﹣b+c<0,其中正确的个数是( ) 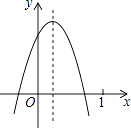
A.4个
B.3个
C.2个
D.1个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC 中,AB=AC,CD是∠ACB的平分线,DE∥BC,交AC于点 E.
(1)求证:DE=CE.
(2)若∠CDE=35°,求∠A 的度数.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】作图题(不写作法,保留作图痕迹):
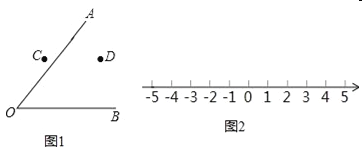
(1)尺规作图:校园有两条路OA、OB,在交叉路口附近有两块宣传牌C、D,学校准备在这里安装一盏路灯,要求灯柱的位置P离两块宣传牌一样远,并且到两条路的距离也一样远,请你帮助画出灯柱的位置P(如图1).(不写画图过程,保留作图痕迹)
(2)用直尺和圆规在如图2所示的数轴上作出表示![]() 的点.
的点.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】铁路上![]() 、
、![]() 两点相距25km,
两点相距25km,![]() 为良村庄,
为良村庄,![]() 于
于![]() ,
,![]() 于
于![]() ,已知
,已知![]() ,
,![]() ,现在要在铁路
,现在要在铁路![]() 上修建一个土特产收购站
上修建一个土特产收购站![]() .
.

(1)在图![]() 中,若
中,若![]() ,则
,则![]() 战应修建在离
战应修建在离![]() 站多少千米处.
站多少千米处.
(2)在图![]() 中,若
中,若![]() 值最小,则
值最小,则![]() 点应建在哪里,请求出这个最小值.
点应建在哪里,请求出这个最小值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AD为∠BAC的平分线,DE⊥AB于E,DF⊥AC于F,
(1)证明AE=AF;
(2)若△ABC面积是36cm2,AB=10cm,AC=8cm,求DE的长.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com