
【题目】如图,在△ABC 中,AB=AC,CD是∠ACB的平分线,DE∥BC,交AC于点 E.
(1)求证:DE=CE.
(2)若∠CDE=35°,求∠A 的度数.

【答案】(1)见解析;(2) 40°.
【解析】
(1)根据角平分线的性质可得出∠BCD=∠ECD,由DE∥BC可得出∠EDC=∠BCD,进而可得出∠EDC=∠ECD,再利用等角对等边即可证出DE=CE;
(2)由(1)可得出∠ECD=∠EDC=35°,进而可得出∠ACB=2∠ECD=70°,再根据等腰三角形的性质结合三角形内角和定理即可求出∠A的度数.
(1)∵CD是∠ACB的平分线,∴∠BCD=∠ECD.
∵DE∥BC,∴∠EDC=∠BCD,∴∠EDC=∠ECD,∴DE=CE.
(2)∵∠ECD=∠EDC=35°,∴∠ACB=2∠ECD=70°.
∵AB=AC,∴∠ABC=∠ACB=70°,∴∠A=180°﹣70°﹣70°=40°.


科目:初中数学 来源: 题型:
【题目】如图,在正方形网格中,每个小正方形的边长都是1,每个小正方形的顶点叫做格点.网格中有一个格点△ABC(即三角形的顶点都在格点上).
(1)在图中作出△ABC关于直线l对称的△A1B1C1 (要求A与A1,B与B1,C与C1相对应);
(2)求△ABC的面积;
(3)在直线l上找一点P,使得△PAC的周长最小.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,二次函数y=﹣x2+3x+m的图象与x轴的一个交点为B(4,0),另一个交点为A,且与y轴相交于C点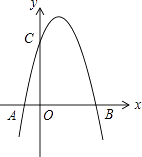
(1)求m的值及C点坐标;
(2)在直线BC上方的抛物线上是否存在一点M,使得它与B,C两点构成的三角形面积最大,若存在,求出此时M点坐标;若不存在,请简要说明理由
(3)P为抛物线上一点,它关于直线BC的对称点为Q
①当四边形PBQC为菱形时,求点P的坐标;
②点P的横坐标为t(0<t<4),当t为何值时,四边形PBQC的面积最大,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,BO、CO分别平分∠ABC和∠ACB.计算:
(1)若∠A=60°,求∠BOC的度数;
(2)若∠A=100°,则∠BOC的度数是多少?
(3)若∠A=120°,则∠BOC的度数又是多少?
(4)由(1)、(2)、(3),你发现了什么规律?请用一个等式将这个规律表示出来.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图四边形ABCD中,AD∥BC,∠BCD=90°,∠BAD的平分线AG交BC于点G.
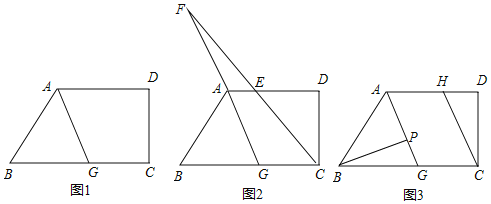
(1)求证:∠BAG=∠BGA;
(2)如图2,∠BCD的平分线CE交AD于点E,与射线GA相交于点F,∠B=50°.
①若点E在线段AD上,求∠AFC的度数;
②若点E在DA的延长线上,直接写出∠AFC的度数;
(3)如图3,点P在线段AG上,∠ABP=2∠PBG,CH∥AG,在直线AG上取一点M,使∠PBM=∠DCH,请直接写出∠ABM:∠PBM的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某镇水库的可用水量为12000万m3,假设年降水量不变,能维持该镇16万人20年的用水量.为实施城镇化建设,新迁入了4万人后,水库只能够维持居民15年的用水量.
(1)问:年降水量为多少万m3?每人年平均用水量多少m3?
(2)政府号召节约用水,希望将水库的使用年限提高到25年.则该镇居民人均每年需节约多少m3水才能实现目标?
(3)某企业投入1000万元设备,每天能淡化5000m3海水,淡化率为70%.每淡化1m3海水所需的费用为1.5元,政府补贴0.3元.企业将淡化水以3.2元/m3的价格出售,每年还需各项支出40万元.按每年实际生产300天计算,该企业至少几年后能收回成本(结果精确到个位)?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知MB=ND,∠MBA=∠NDC,下列条件中不能判定△ABM≌△CDN的是( )

A. ∠M=∠N B. AM=CN C. AB=CD D. AM∥CN
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】重庆市2017年女子迷你马拉松比赛在南滨路举行,王老师和刘老师参加了比赛,图中AB、OC分别表示王老师和刘老师前往终点所跑的路程S(km)随时间t(min)变化的函数图象,以下说法:①这是全长为5km的比赛;②王老师比刘老师早15分钟到达终点;③王老师出发15分钟时遇到刘老师;④王老师的平均速度为500米/分钟.其中正确的有( )

A. ①②③ B. ①②④ C. ①③④ D. ②③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线y=5x+5交x轴于点A,交y轴于点C,过A,C两点的二次函数y=ax2+4x+c的图象交x轴于另一点B.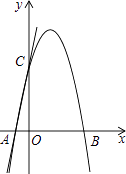
(1)求二次函数的表达式;
(2)连接BC,点N是线段BC上的动点,作ND⊥x轴交二次函数的图象于点D,求线段ND长度的最大值;
(3)若点H为二次函数y=ax2+4x+c图象的顶点,点M(4,m)是该二次函数图象上一点,在x轴、y轴上分别找点F,E,使四边形HEFM的周长最小,求出点F,E的坐标.
温馨提示:在直角坐标系中,若点P,Q的坐标分别为P(x1 , y1),Q(x2 , y2),
当PQ平行x轴时,线段PQ的长度可由公式PQ=|x1﹣x2|求出;
当PQ平行y轴时,线段PQ的长度可由公式PQ=|y1﹣y2|求出.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com