
����Ŀ����ͼ�����κ���y=��x2+3x+m��ͼ����x���һ������ΪB��4��0������һ������ΪA������y���ཻ��C��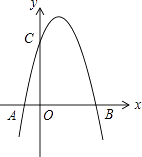
��1����m��ֵ��C�����ꣻ
��2����ֱ��BC�Ϸ������������Ƿ����һ��M��ʹ������B��C���㹹�ɵ������������������ڣ������ʱM�����ꣻ�������ڣ����Ҫ˵������
��3��PΪ��������һ�㣬������ֱ��BC�ĶԳƵ�ΪQ
�ٵ��ı���PBQCΪ����ʱ�����P�����ꣻ
�ڵ�P�ĺ�����Ϊt��0��t��4������tΪ��ֵʱ���ı���PBQC����������˵�����ɣ�
���𰸡�
��1��
�⣺��B��4��0������y=��x2+3x+m��
��ã�m=4��
����κ�������ʽΪy=��x2+3x+4��
��x=0����y=4��
��C��0��4����
��2��
�⣺���ڣ�
���ɣ���B��4��0����C��0��4����
��ֱ��BC����ʽΪy=��x+4��
��ֱ��BC����ƽ��b��λ���������ֻ��һ��������ʱ����MBC������
�� ![]() ��
��
��x2��4x+b=0��
���=14��4b=0��
��b=4��
�� ![]() ��
��
��M��2��6��
��3��
�⣺����ͼ��
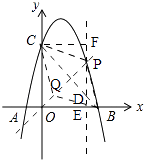
�ߵ�P���������ϣ�
����P��m����m2+3m+4����
���ı���PBQC������ʱ����P���߶�BC�Ĵ�ֱƽ�����ϣ�
��B��4��0����C��0��4��
���߶�BC�Ĵ�ֱƽ���ߵĽ���ʽΪy=x��
��m=��m2+3m+4��
��m=1�� ![]() ��
��
��P��1+ ![]() ��1+
��1+ ![]() ����P��1��
����P��1�� ![]() ��1��
��1�� ![]() ����
����
����ͼ��
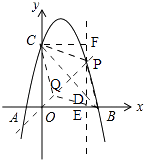
���P��t����t2+3t+4����
����P��y���ƽ����l������C��l�Ĵ��ߣ�
�ߵ�D��ֱ��BC�ϣ�
��D��t����t+4����
��PD=��t2+3t+4������t+4��=��t2+4t��
BE+CF=4��
��S�ı���PBQC=2S��PDC=2��S��PCD+S��BD��=2�� ![]() PD��CF+
PD��CF+ ![]() PD��BE��=4PD=��4t2+16t��
PD��BE��=4PD=��4t2+16t��
��0��t��4��
�൱t=2ʱ��S�ı���PBQC���=16
����������1���ô���ϵ������������߽���ʽ����2�����жϳ�������ʱ��ƽ��ֱ��BC��ֱ�ߺ�������ֻ��һ�����㣬�Ӷ������M���ꣻ��3�������жϳ��ı���PBQCʱ����ʱ����P���߶�BC�Ĵ�ֱƽ���ߣ����ø������Խ���������⣻��������ı���PBCQ�������t�ĺ�����ϵʽ���Ӷ�ȷ�����������ֵ�������Ƕ��κ����ۺ��⣬��Ҫ�����˴���ϵ��������ֵ��ȷ�����Գ��ԣ������ȷ�����Ȿ��Ĺؼ���ȷ������MBC������ʱ����P�����꣮



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ѧ������Ϻ������.
��ĸ�к���δ֪���IJ���ʽ�з�ʽ����ʽ.�磺![]() ��
��![]() ��.��ô���������ǵĽ⼯�أ���������ѧ�������������������֪�����������ͬ�ŵ�������ŵø�.����ĸ����ʽΪ��
��.��ô���������ǵĽ⼯�أ���������ѧ�������������������֪�����������ͬ�ŵ�������ŵø�.����ĸ����ʽΪ��
(1)��![]() ��0��
��0��![]() ��0����
��0����![]() ��0����
��0����![]() ��0��
��0��![]() ��0����
��0����![]() ��0��
��0��
(2)��![]() ��0��
��0��![]() ��0����
��0����![]() ��0����
��0����![]() ��0��
��0��![]() ��0����
��0����![]() ��0.
��0.
��֮��(1)��![]() ��0����
��0����![]() ��
��![]()
(2)��![]() ��0����__________��__________.
��0����__________��__________.
(3)�����������ɣ���ʽ![]() �Ľ⼯.
�Ľ⼯.
(4)����ʽ![]() �Ľ⼯.
�Ľ⼯.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
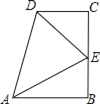
����Ŀ������ѧ����ϣ�С���������һ�����⣺��B=��C=90�㣬E��BC���е㣬DEƽ����ADC����ͼ�����һ�����ҵ����۽�����СӢ��һ���ó����½��ۣ���1��AEƽ����DAB����2����EBA�ա�DCE����3��AB+CD=AD����4��AE��DE����5��AB��CD��������ȷ�Ľ�����_____����������Ϊ��ȷ���۵���Ŷ����ϣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���Ķ����ϣ��������Ǻ����������µĹ�ʽ��
sin�������£�=sin��cos�¡�cos��sin��
tan�������£�= ![]()
������Щ��ʽ���Խ�һЩ��������ǵ����Ǻ���ת��Ϊ����ǵ����Ǻ�������ֵ��
����tan75��=tan��45��+30�㣩= ![]() =
=  =2+
=2+ ![]()
���������Ķ����ϣ���ѡ���ʵ��Ĺ�ʽ�����������
��1�����㣺sin15�㣻
��2��ijУ�ڿ�չ�������������У�������ʿ���ǰ�廳�ͼ���Ϊ�������ĺ��սʿ������ͬѧ������ѧ֪ʶ��������ͼ����ĸ߶ȣ���֪����վ��������7��C������D���ü������������Ϊ75�㣬DCΪ ![]() �ף�������������������ĸ߶ȣ�
�ף�������������������ĸ߶ȣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������ABCD�Ƶ�B��ʱ����ת30���õ�����A1BC1D1 �� C1D1��AD���ڵ�M���ӳ�DA��A1D1��F����AB=1��BC= ![]() ����AF�ij���Ϊ�� ��
����AF�ij����� �� 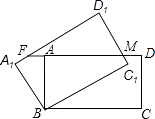
A.2�� ![]()
B.![]()
C.![]()
D.![]() ��1
��1
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ�����ı���ABCD�У��Խ���ACƽ����DAB����ABD=52�㣬��ABC=116�㣬��ACB=���㣬����BDC�Ķ���Ϊ��������

A. �� B. ![]() �� C. 90���� D. 90��
�� C. 90���� D. 90��![]() ��
��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����һ����������һ�����ϵĸߵ��������ߵ�һ�룬��ô���ǰ���������ν�����������Σ���ֱ֪��������![]() �ǰ�������Σ���б��
�ǰ�������Σ���б��![]() ���������ܳ�����_________��
���������ܳ�����_________��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ڡ�ABC �У�AB=AC��CD�ǡ�ACB��ƽ���ߣ�DE��BC����AC�ڵ� E��
��1����֤��DE=CE��
��2������CDE=35�㣬���A �Ķ�����

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��Ϊȷ����Ϣ��ȫ���ڴ���ʱ��������ܣ����ͷ�����һ������a��b��cʱ������շ���Ӧ�յ�������ΪA��B��C��˫��Լ����A=2a��b��B=2b��C=b+c�����緢��1��2��3�����յ�0��4��5
��1�������ͷ�����һ������Ϊ2��3��5ʱ������շ��յ��������Ƕ��٣�
��2�������շ��յ�һ������2��8��11ʱ�����ͷ������������Ƕ��٣�
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com