
【题目】铁路上![]() 、
、![]() 两点相距25km,
两点相距25km,![]() 为良村庄,
为良村庄,![]() 于
于![]() ,
,![]() 于
于![]() ,已知
,已知![]() ,
,![]() ,现在要在铁路
,现在要在铁路![]() 上修建一个土特产收购站
上修建一个土特产收购站![]() .
.

(1)在图![]() 中,若
中,若![]() ,则
,则![]() 战应修建在离
战应修建在离![]() 站多少千米处.
站多少千米处.
(2)在图![]() 中,若
中,若![]() 值最小,则
值最小,则![]() 点应建在哪里,请求出这个最小值.
点应建在哪里,请求出这个最小值.
【答案】(1)10km.(2)AE=15,E应建在距A15千米处.
【解析】
(1)关键描述语:产品收购站E,使得C、D两村到E站的距离相等,在Rt△DAE和Rt△CBE中,设出AE的长,可将DE和CE的长表示出来,列出等式进行求解即可.
(2)根据题意构造直角三角形D′FC,再由勾股定理求解即可.
(1)设AE=xkm,
∵C、D两村到E站的距离相等,∴DE=CE,即DE2=CE2,
由勾股定理,得152+x2=102+(25-x)2,x=10.
故:E点应建在距A站10千米处.
(2)作D点关于AB的对称点D′,连接D′C,再作D′F⊥BC于点F,此时DE+EC最短,

∵DA=15km,CB=10km,A、B两点相距25km,
∴FC=25km,D′F=25km,
根据题意得,![]()
∴BE=10km
∴AE=15km,
∴E应建在距A15千米处.


 字词句篇与同步作文达标系列答案
字词句篇与同步作文达标系列答案科目:初中数学 来源: 题型:
【题目】如图,△ABC为等腰三角形,AB=AC,∠D=∠E,∠BAD=∠CAE.
(1)写出一对全等的三角形:△ ≌△ ;
(2)证明(1)中的结论;
(3)求证:点G为BC的中点.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图四边形ABCD中,AD∥BC,∠BCD=90°,∠BAD的平分线AG交BC于点G.
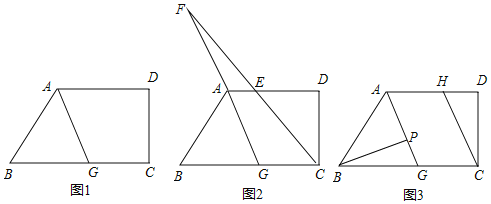
(1)求证:∠BAG=∠BGA;
(2)如图2,∠BCD的平分线CE交AD于点E,与射线GA相交于点F,∠B=50°.
①若点E在线段AD上,求∠AFC的度数;
②若点E在DA的延长线上,直接写出∠AFC的度数;
(3)如图3,点P在线段AG上,∠ABP=2∠PBG,CH∥AG,在直线AG上取一点M,使∠PBM=∠DCH,请直接写出∠ABM:∠PBM的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知MB=ND,∠MBA=∠NDC,下列条件中不能判定△ABM≌△CDN的是( )

A. ∠M=∠N B. AM=CN C. AB=CD D. AM∥CN
查看答案和解析>>
科目:初中数学 来源: 题型:
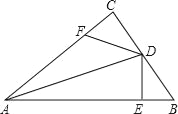
【题目】如图,在△ABC中,∠C=90°,AD平分∠BAC,DE⊥AB于点E,点F在AC上,且BD=DF.
(1)求证:CF=EB;
(2)请你判断AE、AF与BE之间的数量关系,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】重庆市2017年女子迷你马拉松比赛在南滨路举行,王老师和刘老师参加了比赛,图中AB、OC分别表示王老师和刘老师前往终点所跑的路程S(km)随时间t(min)变化的函数图象,以下说法:①这是全长为5km的比赛;②王老师比刘老师早15分钟到达终点;③王老师出发15分钟时遇到刘老师;④王老师的平均速度为500米/分钟.其中正确的有( )

A. ①②③ B. ①②④ C. ①③④ D. ②③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在⊙O中,AB为直径,D、E为圆上两点,C为圆外一点,且∠E+∠C=90°. 
(1)求证:BC为⊙O的切线.
(2)若sinA= ![]() ,BC=6,求⊙O的半径.
,BC=6,求⊙O的半径.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com