Question

【题目】如图，AB=AC，AD=AE，BE、CE相交于点F，则图中全等三角形共有（　　）对．

A. 2 B. 3 C. 4 D. 5

Answer 1

【答案】C

【解析】

先依据等边对等角的性质得到∠ABC=∠ACB，然后再结合全等三角形的判定定理进行判断即可．

连接BC，

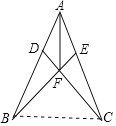
∵AB=AC，AD=AE，

∴∠ABC=∠ACB，BD=EC，

∵在△BDC和△CEB中，，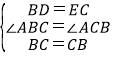

∴△BDC≌△CEB（SAS），

∴∠EBC=∠DCB，

∴∠ABF=∠ACF，

在△DBF和△ECF中，，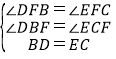

∴△DBF≌△ECF（AAS），

∵∠EBC=∠DCB，

∴FB=FC，

∵在△ABF和△ACF中，，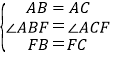

∴△ABF≌△ACF（SAS），

∴∠DAF=∠EAF,

∵在△DAF和△EAF中，，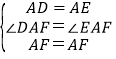

∴△DAF≌△EAF（SAS），

∵在△DAC和△EAB中，，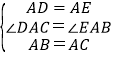

∴△DAC≌△EAB（SAS）．

故选：C．