
分析 (1)令y=0解方程即可求得A和B的横坐标,然后利用配方法即可求得对称轴和顶点坐标;
(2)首先求得D的坐标,然后利用面积公式即可求解.
解答 解:
(1)令y=0,则x2-2x-3=0,
解得:x1=-1,x2=3.
∵点A在点B的左侧.
∴点A的坐标是(-1,0),B的坐标是(3,0).
∵y=--x2-2x-3=(x-1)2-4,
∴抛物线对称轴是x=1;
(2)
∵顶点C的坐标是(1,-4),D与点C关于x轴对称,
∴D的坐标是(1,4).
∴AB=3-(-1)=4,CD=4-(-4)=8,
∴四边形ACBD的面积是:$\frac{1}{2}$AB•CD=$\frac{1}{2}$×4×8=16.
点评 本题考查了待定系数法求函数解析式以及配方法确定二次函数的对称轴和顶点坐标,正确求得A和B的坐标是关键.


 海淀课时新作业金榜卷系列答案
海淀课时新作业金榜卷系列答案 期末金牌卷系列答案
期末金牌卷系列答案 轻松课堂标准练系列答案
轻松课堂标准练系列答案科目:初中数学 来源: 题型:选择题
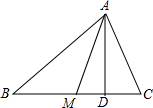 三角形的一个顶点与对边中点的连线称三角形的中线,这条中线关于这个顶角的平分线对称的直线称为三角形的共轭中线,对于共轭中线下列说法正确的序号是( )
三角形的一个顶点与对边中点的连线称三角形的中线,这条中线关于这个顶角的平分线对称的直线称为三角形的共轭中线,对于共轭中线下列说法正确的序号是( )| A. | ①② | B. | ①②④ | C. | ①③④ | D. | ①②③④ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
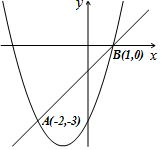 如图,二次函数y=ax2+bx+c(a≠0)和一次函数y=x-1的图象交于A(-2,-3)、B(1,0)两点,则方程ax2+(b-1)x+c+1=0的根为( )
如图,二次函数y=ax2+bx+c(a≠0)和一次函数y=x-1的图象交于A(-2,-3)、B(1,0)两点,则方程ax2+(b-1)x+c+1=0的根为( )| A. | x1=-2,x2=-3 | B. | x1=1,x2=0 | C. | x1=-2,x2=1 | D. | x1=-3,x2=0 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 已知二次函数y=x2+bx+c的图象与y轴交于点C(0,-3),与x轴的一个交点坐标是A(-1,0).
已知二次函数y=x2+bx+c的图象与y轴交于点C(0,-3),与x轴的一个交点坐标是A(-1,0).查看答案和解析>>
科目:初中数学 来源: 题型:选择题
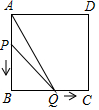 如图,在边长为4的正方形ABCD中,动点P从A点出发,以每秒1个单位长度的速度沿AB向B点运动,同时动点Q从B点出发,以每秒2个单位长度的速度沿BC→CD方向运动,当P运动到B点时,P、Q两点同时停止运动.设P点运动的时间为t秒,△APQ的面积为S,则表示S与t之间的函数关系的图象大致是( )
如图,在边长为4的正方形ABCD中,动点P从A点出发,以每秒1个单位长度的速度沿AB向B点运动,同时动点Q从B点出发,以每秒2个单位长度的速度沿BC→CD方向运动,当P运动到B点时,P、Q两点同时停止运动.设P点运动的时间为t秒,△APQ的面积为S,则表示S与t之间的函数关系的图象大致是( )| A. | 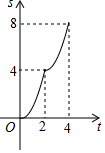 | B. | 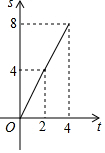 | C. | 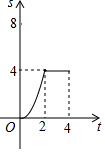 | D. | 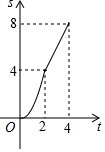 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
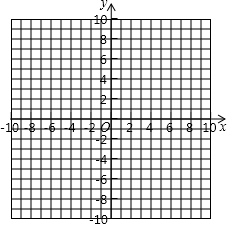 在如图的平面直角坐标系中作△ABC,使点A、B、C的坐标分别为A(4,6),B(0,2),C(6,0),并作出△ABC关于y轴的对称图形.
在如图的平面直角坐标系中作△ABC,使点A、B、C的坐标分别为A(4,6),B(0,2),C(6,0),并作出△ABC关于y轴的对称图形.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com