
 三角形的一个顶点与对边中点的连线称三角形的中线,这条中线关于这个顶角的平分线对称的直线称为三角形的共轭中线,对于共轭中线下列说法正确的序号是( )
三角形的一个顶点与对边中点的连线称三角形的中线,这条中线关于这个顶角的平分线对称的直线称为三角形的共轭中线,对于共轭中线下列说法正确的序号是( )| A. | ①② | B. | ①②④ | C. | ①③④ | D. | ①②③④ |
分析 根据三角形的角平分线、中线和高的定义以及翻折变换的性质进行判断即可.
解答  解:∵等腰三角形底边上的中线、高、角平分线“三线合一”,
解:∵等腰三角形底边上的中线、高、角平分线“三线合一”,
∴等腰三角形底边上的共轭中线就是它的高,①正确;
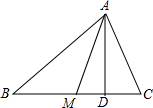
如图1,∠BAC=90°,AM是BC边上的中线,
∴MA=MB,
∴∠BAM=∠A,
由题意和翻折变换的性质可知,∠BAM=∠CAD,
∵∠B+∠C=90°,
∴∠CAD+∠C=90°,即DA⊥BC,
则直角三角形斜边上的高线就是斜边的共轭中线,②正确;
③错误;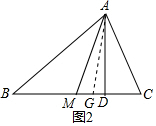
如图2,作∠BAC的平分线AG,
则∠BAG=∠CAG,
由翻折变换的性质可知,∠MAG=∠DAG,
∴∠BAM=∠CAD,④正确,
故选B.
点评 本题考查的是三角形的角平分线、中线和高,从三角形的一个顶点向底边作垂线,垂足与顶点之间的线段叫做三角形的高,三角形一个内角的平分线与这个内角的对边交于一点,则这个内角的顶点与所交的点间的线段叫做三角形的角平分线,三角形一边的中点与此边所对顶点的连线叫做三角形的中线.


科目:初中数学 来源: 题型:填空题
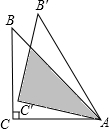 如图,等腰Rt△ABC中,∠C=90°,BC=6cm,将△ABC绕点A顺时针旋转15°后得到△AB′C′,则图中阴影部分的面积是6$\sqrt{3}$cm2.
如图,等腰Rt△ABC中,∠C=90°,BC=6cm,将△ABC绕点A顺时针旋转15°后得到△AB′C′,则图中阴影部分的面积是6$\sqrt{3}$cm2.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com