
【题目】如图,已知四边形ABCD是矩形,且MO=MD=4,MC=3.
(1)求直线BM的解析式;
(2)求过A、M、B三点的抛物线的解析式;
(3)在(2)中的抛物线上是否存在点P,使△PMB构成以BM为直角边的直角三角形?若没有,请说明理由;若有,则求出一个符合条件的P点的坐标.

【答案】(1)y=-![]() x+4.(2)y=-
x+4.(2)y=-![]() x2-
x2-![]() x+4;(3)见解析(-
x+4;(3)见解析(-![]() )(-
)(-![]() ).
).
【解析】
(1)根据MO=MD=4,MC=3就可以求出A、M、B三点的作坐标,根据待定系数法就可以求出直线BM的解析式与抛物线的解析式.
(2)根据(1)中A、M、B三点的作坐标,根据待定系数法就可以求出抛物线的解析式.
(3)过M、B作MB的垂线,它与抛物线的交点即为P点,因而符合条件的P点是存在的.当∠PMB=90°时,过P作PH⊥DC交于H,则可证△MPH∽△BMC,得到PH:HM=CM:CB=3:4,因而可以设HM=4a(a>0),则PH=3a,则P点的坐标为(-4a,4-3a).将P点的坐标代入y=-![]() x2-
x2-![]() +4就可以求出a的值,进而求出P点的坐标.
+4就可以求出a的值,进而求出P点的坐标.
解:(1)∵MO=MD=4,MC=3,
∴M、A、B的坐标分别为(0,4),(-4,0),(3,0)
设BM的解析式为y=kx+b;
则![]() ,解得:
,解得: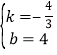
∴BM的解析式为y=![]() x+4.
x+4.
(2)设抛物线的解析式为y=a(x+4)(x-3)
将M(0,4)的坐标代入得a=-![]()
∴y=-![]() (x+4)(x-3)=-
(x+4)(x-3)=-![]() x2-
x2-![]() x+4
x+4
(3)设抛物线上存在点P,使△PMB构成直角三角形.
①过M作MB的垂线与抛物线交于P,过P作PH⊥DC交于H,
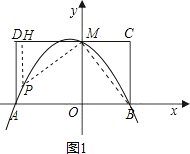
∴∠PMB=90°,
∴∠PMH=∠MBC,
∴△MPH∽△BMC,
∴PH:HM=CM:CB=3:4
设HM=4a(a>0),则PH=3a
∴P点的坐标为(-4a,4-3a)
将P点的坐标代入y=-![]() x2-
x2-![]() x+4得:
x+4得:
4-3a=-![]() (-4a)2-
(-4a)2-![]() ×(-4a)+4
×(-4a)+4
解得a=0(舍出),a=![]() ,
,
∴P点的坐标为(-![]() ,
,![]() )
)
②或者,抛物线上存在点P,使△PMB构成直角三角形.
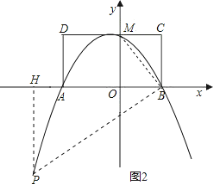
过M作MB的垂线与抛物线交于P,设P的坐标为(x0,y0),
由∠PMB=90°,∠PMD=∠MBC,
过P作PH⊥DC交于H,则MH=-x0,PH=4-y0
∴由tan∠PMD=tan∠MBC
得![]() =
=![]() ,
,
∴![]() =
=![]() +4
+4
∴![]() +4=-
+4=-![]() -
-![]() +4
+4
∴![]() ,
,![]() =0(舍去)
=0(舍去)
∴![]() =
=![]() (
(![]() )+4=
)+4=![]() ,
,
∴P点的坐标为(![]() ,
,![]() )
)
类似的,如果过B作BM的垂线与抛物线交于点P,
设P的坐标为(x0,y0),
同样可求得![]() =
=![]() -
-![]() ,
,
由![]() -
-![]() =-
=-![]() -
-![]() +4
+4
∴![]() ,
,![]() =3(舍去)
=3(舍去)
![]() =
=![]() (
(![]() )-
)-![]() =-
=-![]()
这时P的坐标为(![]() ,-
,-![]() ).
).


科目:初中数学 来源: 题型:
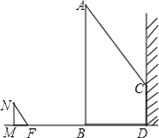
【题目】如图,一电线杆AB的影子分别落在了地上和墙上.同一时刻,小明竖起1米高的直杆MN,量得其影长MF为0.5米,量得电线杆AB落在地上的影子BD长3米,落在墙上的影子CD的高为2米.你能利用小明测量的数据算出电线杆AB的高吗?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】被誉为“中原第一高楼”的郑州会展宾馆(俗称“玉米楼”)坐落在风景如画的如意湖畔,是来郑州观光的游客留影的最佳景点.学完了三角函数知识后,刘明和王华决定用自己学到的知识测量“玉米楼”的高度.如图,刘明在点C处测得楼顶B的仰角为45°,王华在高台上的D处测得楼顶的仰角为40°.若高台DE的高为5米,点D到点C的水平距离EC为47.4米,A,C,E三点共线,求“玉米楼”AB的高度.(参考数据:sin40°≈0.64,cos40°≈0.77,tan40°≈0.84,结果保留整数)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某幢建筑物,从10米高的窗口A用水管和向外喷水,喷的水流呈抛物线(抛物线所在平面与墙面垂直),(如图)如果抛物线的最高点M离墙1米,离地面![]() 米,则水流下落点B离墙距离OB是( )
米,则水流下落点B离墙距离OB是( )

A. 2米 B. 3米 C. 4米 D. 5米
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某种电热淋浴器的水箱盛满水时有200升,加热到一定温度即可供淋浴用,在放水的同时自动注水,设t分钟内注水2t2升,放水34t升,当水箱内的水量达到最小值时,必须停止放水并将水箱注满,加热升温,过一定时间后,才能继续放水使用,现规定每人洗浴用水量不得超过60升,请回答下列问题:
(1)求水箱内水量的最小值;
(2)说明该淋浴器一次可连续供几人洗浴.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,扇形OAB中,∠AOB=60°,扇形半径为4,点C在![]() 上,CD⊥OA,垂足为点D,当△OCD的面积最大时,图中阴影部分的面积为_____.
上,CD⊥OA,垂足为点D,当△OCD的面积最大时,图中阴影部分的面积为_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
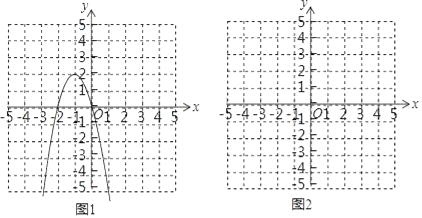
【题目】根据下列要求,解答相关问题:
(1)请补全以下求不等式﹣2x2﹣4x≥0的解集的过程
①构造函数,画出图象:
根据不等式特征构造二次函数y=﹣2x2﹣4x;抛物线的对称轴x=﹣1,开口向下,顶点(﹣1,2)与x轴的交点是(0,0),(﹣2,0),用三点法画出二次函数y=﹣2x2﹣4x的图象如图1所示;
②数形结合,求得界点:
当y=0时,求得方程﹣2x2﹣4x=0的解为 ;
③借助图象,写出解集:
由图象可得不等式﹣2x2﹣4x≥0的解集为 .
(2)利用(1)中求不等式解集的方法步骤,求不等式x2﹣2x+1<4的解集.
①构造函数,画出图象;
②数形结合,求得界点;
③借助图象,写出解集.
(3)参照以上两个求不等式解集的过程,借助一元二次方程的求根公式,直接写出关于x的不等式ax2+bx+c>0(a>0)的解集.
查看答案和解析>>
科目:初中数学 来源: 题型:
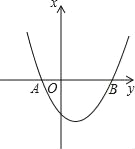
【题目】抛物线y=x2+bx+c与x轴交于A(﹣1,0),B(3,0)两点.
(1)求该抛物线的解析式.
(2)一动点P在(1)中抛物线上滑动且满足S△ABP=10,求此时P点的坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com