
【题目】如图,扇形OAB中,∠AOB=60°,扇形半径为4,点C在![]() 上,CD⊥OA,垂足为点D,当△OCD的面积最大时,图中阴影部分的面积为_____.
上,CD⊥OA,垂足为点D,当△OCD的面积最大时,图中阴影部分的面积为_____.

科目:初中数学 来源: 题型:
【题目】已知:在△ABC中,AB=4,BC=5,CA=6.
(1)如果DE=10,那么当EF=________,FD=________时,△DEF∽△ABC;
(2)如果DE=10,那么当EF=________,FD=________时,△FDE∽△ABC.
查看答案和解析>>
科目:初中数学 来源: 题型:
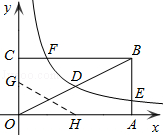
【题目】如图,矩形OABC的顶点A、C分别在x、y轴的正半轴上,点D为对角线OB的中点,点E(4,n)在边AB上,反比例函数![]() (k≠0)在第一象限内的图象经过点D、E,且tan∠BOA=
(k≠0)在第一象限内的图象经过点D、E,且tan∠BOA=![]() .
.
(1)求边AB的长;
(2)求反比例函数的解析式和n的值;
(3)若反比例函数的图象与矩形的边BC交于点F,将矩形折叠,使点O与点F重合,折痕分别与x、y轴正半轴交于点H、G,求线段OG的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
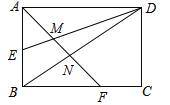
【题目】如图,矩形ABCD的边长AD=3,AB=2,E为AB的中点,F在边BC上,且BF=2FC,AF分别与DE、DB相交于点M,N,则MN的长为( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知四边形ABCD是矩形,且MO=MD=4,MC=3.
(1)求直线BM的解析式;
(2)求过A、M、B三点的抛物线的解析式;
(3)在(2)中的抛物线上是否存在点P,使△PMB构成以BM为直角边的直角三角形?若没有,请说明理由;若有,则求出一个符合条件的P点的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(9分)如图,AB是半圆O的直径,点P是半圆上不与点A、B重合的一个动点,延长BP到点C,使PC=PB,D是AC的中点,连接PD,PO.
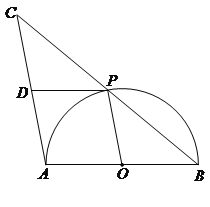
(1)求证:△CDP≌△POB;
(2)填空:
① 若AB=4,则四边形AOPD的最大面积为 ;
② 连接OD,当∠PBA的度数为 时,四边形BPDO是菱形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某药品研究所开发一种抗菌新药,经多年动物实验,首次用于临床人体试验,测得成人服药后血液中药物浓度y(微克/毫升)与服药时间x小时之间函数关系如图所示(当4≤x≤10时,y与x成反比例).
(1)根据图象分别求出血液中药物浓度上升和下降阶段y与x之间的函数关系式.
(2)问血液中药物浓度不低于2微克/毫升的持续时间多少小时?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】名闻遐迩的采花毛尖明前茶,成本每厅400元,某茶场今年春天试营销,每周的销售量y(斤)是销售单价x(元/斤)的一次函数,且满足如下关系:
x(元/斤) | 450 | 500 | 600 |
y(斤) | 350 | 300 | 200 |
(1)请根据表中的数据求出y与x之间的函数关系式;
(2)若销售每斤茶叶获利不能超过40%,该茶场每周获利不少于30000元,试确定销售单价x的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,△ABC 顶点 A(2,3).若以原点 O 为位似中心,画三角形 ABC
的位似图形△A′B′C′,使△ABC 与△A′B′C′的相似比为![]() ,则 A′的坐标为( )
,则 A′的坐标为( )
A. (3,![]() ) B. (
) B. (![]() ,6) C. (3,
,6) C. (3,![]() )或(-3,-
)或(-3,-![]() ) D. (
) D. (![]() ,6)或(-
,6)或(-![]() ,-6)
,-6)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com