
【题目】在平面直角坐标系中,△ABC 顶点 A(2,3).若以原点 O 为位似中心,画三角形 ABC
的位似图形△A′B′C′,使△ABC 与△A′B′C′的相似比为![]() ,则 A′的坐标为( )
,则 A′的坐标为( )
A. (3,![]() ) B. (
) B. (![]() ,6) C. (3,
,6) C. (3,![]() )或(-3,-
)或(-3,-![]() ) D. (
) D. (![]() ,6)或(-
,6)或(-![]() ,-6)
,-6)
科目:初中数学 来源: 题型:
【题目】如图,扇形OAB中,∠AOB=60°,扇形半径为4,点C在![]() 上,CD⊥OA,垂足为点D,当△OCD的面积最大时,图中阴影部分的面积为_____.
上,CD⊥OA,垂足为点D,当△OCD的面积最大时,图中阴影部分的面积为_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
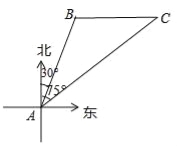
【题目】南海是我国的南大门,如图所示,某天我国一艘海监执法船在南海海域正在进行常态化巡航,在A处测得北偏东30°方向上,距离为20海里的B处有一艘不明身份的船只正在向正东方向航行,便迅速沿北偏东75°的方向前往监视巡查,经过一段时间后,在C处成功拦截不明船只,问我海监执法船在前往监视巡查的过程中行驶了多少海里(最后结果保留整数)?
![]()
![]() (参考数据:cos75°=0.2588,sin75°=0.9659,tan75°=3.732,
(参考数据:cos75°=0.2588,sin75°=0.9659,tan75°=3.732,![]() =1.732,
=1.732,![]() =1.414)
=1.414)
查看答案和解析>>
科目:初中数学 来源: 题型:
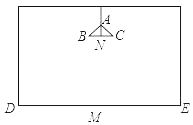
【题目】在长、宽都为4m,高为3m的房间的正中央的天花板上悬挂着一只白炽灯泡,为了集中光线,加上了灯罩(如图所示).已知灯罩深AN=8cm,灯泡离地面2m,为了使光线恰好照在墙角D、E处,灯罩的直径BC应为多少?(结果保留两位小数,![]() ≈1.414)
≈1.414)
查看答案和解析>>
科目:初中数学 来源: 题型:
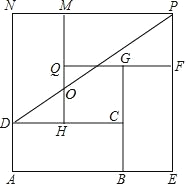
【题目】如图,已知长方形 ABCD 中,AB=a,BC=b.正方形 AEPN 是由长方形 ABCD经过图形的运动形成的.其中长方形 GBEF 是由长方形 ABCD 绕着 B 点顺时针旋转 90° 得到的,长方形 HMND 是由将长方形 ABCD 绕着 D 点逆时针旋转 90°得到的,长方形QFPM 是长方形 ABCD 经过平移得到的.
(1) 长方形 QFPM 是由长方形 ABCD 经过怎样平移得到的?
(2) 用含 a、b 的代数式分别表示正方形 HCGQ 的面积;
(3) 连接 DP,交 HM 于点 O.用 a、b 的代数式分别表示 OM.
查看答案和解析>>
科目:初中数学 来源: 题型:
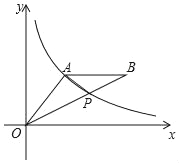
【题目】如图,A(3,m)是反比例函数y=![]() 在第一象限图象上一点,连接OA,过A作AB∥x轴,连接OB,交反比例函数y=
在第一象限图象上一点,连接OA,过A作AB∥x轴,连接OB,交反比例函数y=![]() 的图象于点P(2
的图象于点P(2![]() ,
,![]() ).
).
(1)求m的值和点B的坐标;
(2)连接AP,求△OAP的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】《孙子算经》是中国传统数学最重要的著作,约成书于四、五世纪.现在传本的《孙子算经》共三卷.卷上叙述算筹记数的纵横相间制度和筹算乘除法则;卷中举例说明筹算分数算法和筹算开平方法;卷下记录算题,不但提供了答案,而且还给出了解法.其中记载:“今有木,不知长短.引绳度之,余绳四尺五,屈绳量之,不足一尺.问木长几何?”
译文:“用一根绳子去量一根长木,绳子还剩余4.5尺,将绳子对折再量长木,长木还剩余1尺,问长木长多少尺?”
请解答上述问题.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=4,AC=3.
(1)试在AB上确定点D的位置,△ACD∽△ABC;
(2)试在AC的延长线上确定点E的位置,使△AEB∽△ABC,此时BE与DC有怎样的位置关系?为什么?

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com