
【题目】如图,四边形ABCD是正方形,点E是边BC的中点,∠AEF=90°,且EF交正方形外角的平分线CF于点F.

(1)求证:AE=EF.
(2)(探究1)变特殊为一般:若题中“点E是边BC的中点”变为“点E是BC边上任意一点”,则上述结论是否仍然成立?(填“是”或“否”).
(3)(探究2)在探究1的前提下,若题中结论“AE=EF”与条件“CF是正方形外角的平分线”互换,则命题是否还成立?请给出证明.
【答案】(1)见解析;(2)是;(3)仍然成立,见解析
【解析】
(1)取AB中点M,连接EM,求出BM=BE,得出∠BME=45°,求出∠AME=∠ECF=135°,求出∠MAE=∠FEC,根据ASA推出△AME和△ECF全等即可;
(2)截取BE=BM,连接EM,求出AM=EC,得出∠BME=45°,求出∠AME=∠ECF=135°,求出∠MAE=∠FEC,根据ASA推出△AME和△ECF全等即可;
(3)过点F作FH⊥BC,交BC的延长线于点H,得到∠BAE=∠HEF,再证明△ABE≌△EHF可得出BE=CH,FH=CH,从而得到∠HFC=∠DCF=45°,即可得出结论.
解:(1)证明:取AB的中点M,连接ME,如图1,
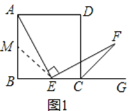
∴AM=BM=![]() AB.
AB.
∵E是BC的中点,
∴BE=EC=![]() BC.
BC.
∵四边形ABCD是正方形,
∴∠B=∠BCD=90°,AB=BC.
∴AM=EC,BM=BE.
∴∠BME=45°.
∴∠AME=135°.
又∵CF是正方形外角的平分线,
∴∠ECF=135°.
∵∠AEF=90°,
∴∠AEB+∠FEC=90°.
又∵∠AEB+∠BAE=90°,
∴∠BAE=∠FEC.
∴△AME≌△ECF(ASA).
∴AE=EF.
(2)【探究1】变特殊为一般:若题中“点E是边BC的中点”变为“点E是BC边上任意一点”,则上述结论仍然成立.
理由是:如图2,在AB上截取BM=BE,连接ME,
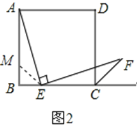
∵∠B=90°,
∴∠BME=∠BEM=45°,
∴∠AME=135°=∠ECF,
∵AB=BC,BM=BE,
∴AM=EC,
在△AME和△ECF中
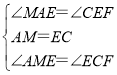 ,
,
∴△AME≌△ECF(ASA),
∴AE=EF;
(3)【探究2】在探究1的前提下,若题中结论“AE=EF”与条件“CF是正方形外角的平分线”互换,则命题仍然成立.
证明:过点F作FH⊥BC,交BC的延长线于点H,如图3,

∵∠AEF=90°,
∴∠AEB+∠FEH=90°.
∵∠ABE=90°,
∴∠AEB+∠BAE=90°.
∴∠BAE=∠HEF.
在△ABE和△EHF中,
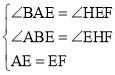
∴△ABE≌△EHF(AAS).
∴BE=HF,AB=EH=BC.
∴BC-EC=EH-EC,即BE=CH.
∴HF=CH.
∴∠HCF=∠HFC=45°,∠DCF=45°.
∴CF是正方形外角的平分线.


 期末集结号系列答案
期末集结号系列答案科目:初中数学 来源: 题型:
【题目】校学生会对七年级部分学生的课外阅读量进行了随机调查,整理调查结果,并根据调查结果绘制了不完整的图表,如图所示:
本数(本) | 频数(人数) | 频率 |
5 | a | 0.3 |
6 | 10 | 0.2 |
7 | 20 | b |
8 | 5 | 0.1 |
合计 | c | 1 |
(1)统计表中的b= ,c= ;请将频数分布直方图补充完整.
(2)所有被调查学生课外阅读的平均本数为 本,课外阅读书本数的中位数为 本.
(3)若该校七年级共有1200名学生,估计该校七年级学生课外阅读6本及以下的人数为 人.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一列快车从甲地驶往乙地,一列慢车从乙地驶往甲地,两车同时出发,匀速行驶,设慢车行驶的时间x(h),两车之间的距离为y(km),图中的折线表示y与x之间的函数关系.根据图象回答:
(1)甲、乙两地之间的距离为 ;
(2)两车同时出发后 h相遇;
(3)慢车的速度为 千米/小时;快车的速度为 千米/小时;
(4)线段CD表示的实际意义是 .

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,请在下列四个关系中,选出两个恰当的关系作为条件,推出四边形ABCD是平行四边形,并予以证明.关系:①AD∥BC;②AB=CD;③∠A=∠C;④∠B+∠C=180°.
(1)写出所有成立的情况(只需填写序号);
(2)选择其中一种证明.
已知:在四边形ABCD中, ;
求证:四边形ABCD是平行四边形.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,已知抛物线y=ax2+bx﹣2(a≠0)与x轴交于A(1,0)、B(3,0)两点,与y轴交于点C,其顶点为点D,点E的坐标为(0,﹣1),该抛物线与BE交于另一点F,连接BC.
(1)求该抛物线的解析式,并用配方法把解析式化为y=a(x﹣h)2+k的形式;
(2)若点H(1,y)在BC上,连接FH,求△FHB的面积;
(3)一动点M从点D出发,以每秒1个单位的速度平沿行与y轴方向向上运动,连接OM,BM,设运动时间为t秒(t>0),在点M的运动过程中,当t为何值时,∠OMB=90°?
(4)在x轴上方的抛物线上,是否存在点P,使得∠PBF被BA平分?若存在,请直接写出点P的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图(1)四边形ABCD中,已知∠ABC+∠ADC=180°,AB=AD,DA⊥AB,点E在CD的延长线上,∠BAC=∠DAE.
(1)求证:△ABC≌△ADE;
(2)求证:CA平分∠BCD;
(3)如图(2),设AF是△ABC的BC边上的高,求证:EC=2AF.

查看答案和解析>>
科目:初中数学 来源: 题型:
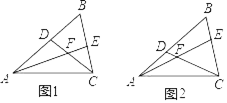
【题目】在△ABC中,∠B=60°,D、E分别为AB、BC上的点,且AE、CD交于点F.
(1)如图1,若AE、CD为△ABC的角平分线:
①求∠AFD的度数;
②若AD=3,CE=2,求AC的长;
(2)如图2,若∠EAC=∠DCA=30°,求证:AD=CE.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】《如果想毁掉一个孩子,就给他一部手机!》这是微信朋友圈热传的一篇文章.国际上,法国教育部宣布从2018年9月新学期起,小学和初中禁止学生使用手机.为了解学生手机使用情况,某学校开展了“手机伴我健康行”主题活动,他们随机抽取部分学生进行“使用手机目的”和“每周使用手机的时间”的问卷调查,并绘制成如图所示的统计图,已知“查资料”的人数是![]() 人.
人.

请你根据以上信息解答下列问题:
![]() 求出本次随机抽取的学生共有多少人;
求出本次随机抽取的学生共有多少人;
![]() 在扇形统计图中,“玩游戏”对应的百分比为______________,圆心角度数是_______________度;
在扇形统计图中,“玩游戏”对应的百分比为______________,圆心角度数是_______________度;
![]() 补全条形统计图;
补全条形统计图;
![]() 该校共有学生
该校共有学生![]() 人,估计每周使用手机时间在
人,估计每周使用手机时间在![]() 小时以上(不含
小时以上(不含![]() 小时)的人数.
小时)的人数.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com