
【题目】一辆客车从甲地开往乙地,一辆轿车从乙地开往甲地,两车同时出发,两车行驶x小时后,记客车离甲地的距离为y1千米,轿车离甲地的距离为y2千米,y1、y2关于x的函数图象如图.
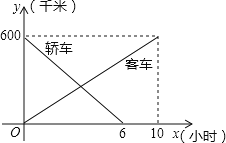
(1)根据图象,直接写出y1、y2关于x的函数关系式;
(2)当两车相遇时,求此时客车行驶的时间;
(3)两车相距200千米时,求客车行驶的时间.
【答案】(1)y2=﹣100x+600 (0≤x≤6);
(2)当两车相遇时,求此时客车行驶了![]() 小时;
小时;
(3)两车相距200千米时,客车行驶的时间为![]() 小时或5小时.
小时或5小时.
【解析】
试题分析:(1)根据图象得出点的坐标,进而利用待定系数法求一次函数解析式得出即可;
(2)当两车相遇时,y1=y2,进而求出即可;
(3)分别根据若相遇前两车相距200千米,则y2﹣y1=200,若相遇后相距200千米,则y1﹣y2=200,分别求出即可.
解:(1)设y1=kx,则将(10,600)代入得出:
600=10k,
解得:k=60,
∴y1=60x (0≤x≤10),
设y2=ax+b,则将(0,600),(6,0)代入得出:
![]()
解得:![]()
∴y2=﹣100x+600 (0≤x≤6);
(2)当两车相遇时,y1=y2,即60x=﹣100x+600
解得:![]() ;
;
∴当两车相遇时,求此时客车行驶了![]() 小时;
小时;
(3)若相遇前两车相距200千米,则y2﹣y1=200,
∴﹣100x+600﹣60x=200,
解得:![]() ,
,
若相遇后相距200千米,则y1﹣y2=200,即60x+100x﹣600=200,
解得:x=5
∴两车相距200千米时,客车行驶的时间为![]() 小时或5小时.
小时或5小时.


科目:初中数学 来源: 题型:
【题目】小明和几位同学做手的影子游戏时,发现对于同一物体,影子的大小与光源到物体的距离有关.因此,他们认为:可以借助物体的影子长度计算光源到物体的位置.于是,他们做了以下尝试.

(1)如图1,垂直于地面放置的正方形框架ABCD,边长AB为30cm,在其正上方有一灯泡,在灯泡的照射下,正方形框架的横向影子A′B,D′C的长度和为6cm.那么灯泡离地面的高度为 .
(2)不改变图1中灯泡的高度,将两个边长为30cm的正方形框架按图2摆放,请计算此时横向影子A′B,D′C的长度和为多少?
(3)有n个边长为a的正方形按图3摆放,测得横向影子A′B,D′C的长度和为b,求灯泡离地面的距离.(写出解题过程,结果用含a,b,n的代数式表示)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】对于实数a,b,如果a>0,b<0且|a|<|b|,那么下列等式成立的是( )
A. a+b=|a|+|b| B. a+b=﹣(|a|+|b|) C. a+b=﹣(|a|﹣|b|) D. a+b=﹣(|b|﹣|a|)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】六月份某登山队在山顶测得温度为零下32度,此时山脚下的温度为零上12度,则山顶的温度比山脚下的温度低( )
A. 20° B. ﹣20℃ C. 44℃ D. ﹣44℃
查看答案和解析>>
科目:初中数学 来源: 题型:
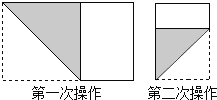
【题目】长为1,宽为a的矩形纸片(![]() ),如图那样折一下,剪下一个边长等于矩形宽度的正方形(称为第一次操作);再把剩下的矩形如图那样折一下,剪下一个边长等于此时矩形宽度的正方形(称为第二次操作);如此反复操作下去.若在第n此操作后,剩下的矩形为正方形,则操作终止.当n=3时,a的值为 .
),如图那样折一下,剪下一个边长等于矩形宽度的正方形(称为第一次操作);再把剩下的矩形如图那样折一下,剪下一个边长等于此时矩形宽度的正方形(称为第二次操作);如此反复操作下去.若在第n此操作后,剩下的矩形为正方形,则操作终止.当n=3时,a的值为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在检测某种品牌奶粉的营养含量的时候,要检验糖、蛋白质、钙、其他物质在奶粉中的百分比含量,已知某次检测的结果是x%,y%,z%,w %,则x+y+z+w=_______.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com