练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】如图所示，在△ABC中，∠ACB＝90°点E是AB的中点，连接CE，过点E作ED⊥BC于点D，在DE的延长线上取一点F，使AF＝CE，求证四边形ACEF是平行四边形．

    【答案】答案见解析

    【解析】试题分析：要证明四边形ACEF是平行四边形，需求证CE∥AF，由已知易得△BEC，△AEF是等腰三角形，则∠1=∠2，∠3=∠F，又∠2=∠3，得到∠1=∠F，故CE∥AF，由此即可得到结论．

    试题解析：证明：∵点E为AB中点，∴AE=EB．又∵∠ACB=90°，∴CE=AE=EB．又∵AF=CE，∴AF=AE，∴∠3=∠F．又∵EB=EC，ED⊥BC，∴∠1=∠2（三线合一）．又∵∠2=∠3，∴∠1=∠F，∴CE∥AF，∴四边形ACEF是平行四边形．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】如图，已知点P在△ABC的边AC上，下列条件中，不能判断△ABP∽△ACB的是（ ）
    A.∠ABP=∠C
    B.∠APB=∠ABC
    C.AB2=AP?AC
    D.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，∠AOB＝∠COD＝90°，OE平分∠BOD，若∠AOD∶∠BOC＝5∶1，则∠COE的度数为(　　)

    A. 30° B. 40° C. 50° D. 60°

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图1，已知点E，F，G，H分别是四边形ABCD各边AB，BC，CD，DA的中点，根据以下思路可以证明四边形EFGH是平行四边形：

    （1）如图2，将图1中的点C移动至与点E重合的位置，F，G，H仍是BC，CD，DA的中点，求证：四边形CFGH是平行四边形；

    （2）如图3，在边长为1的小正方形组成的5×5网格中，点A，C，B都在格点上，在格点上画出点D，使点C与BC，CD，DA的中点F，G，H组成正方形CFGH；

    （3）在（2）条件下求出正方形CFGH的边长．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】一位出租车司机某日中午的营运全在市区的环城公路上进行．如果规定：顺时针方向为正，逆时针方向为负，那天中午他拉了五位乘客所行车的里程如下：（单位：千米）+10，﹣7，+4，﹣9，+2．

    （1）将最后一名乘客送到目的地时，这位司机距离出车地点的位置如何？

    （2）若汽车耗油为升/千米，那么这天中午这辆出租车的油耗多少升？

    （3）如果出租车的收费标准是：起步价10元，3千米后每千米2元，问：这个司机这天中午的收入是多少？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，以AB为直径的⊙O经过点P，C是⊙O上一点，连接PC交AB于点E，且∠ACP=60°，PA=PD．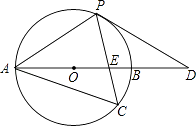
    （1）试判断PD与⊙O的位置关系，并说明理由；
    （2）若 ： =1：2，求AE：EB：BD的值（请你直接写出结果）；
    （3）若点C是弧AB的中点，已知AB=4，求CECP的值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】已知反比例函数的图象经过A(2,-4)．

    (1)求k的值．

    (2)这个函数的图象在哪几个象限？y随x的增大怎样变化？

    (3)画出函数的图象．

    (4)点B(-2,4),C(-1,5)在这个函数的图象上吗？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图所示，OB是∠AOC的平分线，OD是∠COE的平分线．

    (1)若∠AOB＝50°，∠DOE＝35°，求∠BOD的度数；

    (2)若∠AOE＝160°，∠COD＝40°，求∠AOB的度数．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图是一个在平面直角坐标系中从原点开始的回形图，其中回形通道的宽和OA的长都是1.

    (1)观察图形填写表格：

    点

    坐标

    所在象限或坐标轴

    A

    B

    C

    D

    E

    F

    (2)在图上将回形图继续画下去(至少再画出4个拐点)；

    (3)说出回形图中位于第一象限的拐点的横坐标与纵坐标之间的关系；

    (4)观察图形，说出(3)中的关系在第三象限中是否存在？

    查看答案和解析>>

    同步练习册答案