
【题目】如图,斜坡AB长10米,按图中的直角坐标系可用![]() 表示,点A,B分别在x轴和y轴上,且
表示,点A,B分别在x轴和y轴上,且![]() .在坡上的A处有喷灌设备,喷出的水柱呈抛物线形落到B处,抛物线可用
.在坡上的A处有喷灌设备,喷出的水柱呈抛物线形落到B处,抛物线可用![]() 表示.
表示.
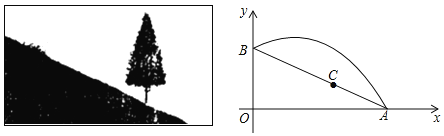
(1)求抛物线的函数关系式(不必写自变量取值范围);
(2)求水柱离坡面AB的最大高度;
(3)在斜坡上距离A点2米的C处有一颗3.5米高的树,水柱能否越过这棵树?
【答案】(1)![]() ;(2)
;(2)![]() 米;(3)水柱能越过树
米;(3)水柱能越过树
【解析】
(1)根据直角三角形的性质求出点A、B的坐标,再利用待定系数法求解可得;
(2)水柱离坡面的距离d=-![]() x2+
x2+![]() x+5-(-
x+5-(-![]() x+5),整理成一般式,再配方成顶点式即可得;
x+5),整理成一般式,再配方成顶点式即可得;
(3)先求出点C的坐标为(4![]() ,1),再求出x=4
,1),再求出x=4![]() 时的函数值y,与1+3.5比较大小即可得.
时的函数值y,与1+3.5比较大小即可得.
(1)∵AB=10、∠OAB=30°,
∴OB=![]() AB=5、OA=ABcos∠OAB=10×
AB=5、OA=ABcos∠OAB=10×![]() =5
=5![]() ,
,
则A(5![]() ,0)、B(0,5),
,0)、B(0,5),
将A、B坐标代入y=-![]() x2+bx+c,得:
x2+bx+c,得:
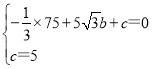 ,
,
解得: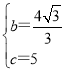 ,
,
∴抛物线解析式为y=-![]() x2+
x2+![]() x+5;
x+5;
(2)水柱离坡面的距离d=-![]() x2+
x2+![]() x+5-(-
x+5-(-![]() x+5)
x+5)
=-![]() x2+
x2+![]() x
x
=-![]() (x2-5
(x2-5![]() x)
x)
=-![]() (x-
(x-![]() )2+
)2+![]() ,
,
∴当x=![]() 时,水柱离坡面的距离最大,最大距离为
时,水柱离坡面的距离最大,最大距离为![]() 米;
米;
(3)如图,过点C作CD⊥OA于点D,
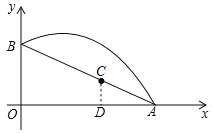
∵AC=2、∠OAB=30°,
∴CD=1、AD=![]() ,
,
则OD=4![]() ,
,
当x=4![]() 时,y=-
时,y=-![]() ×(4
×(4![]() )2+
)2+![]() ×4
×4![]() +5=5>1+3.5,
+5=5>1+3.5,
所以水柱能越过树.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】如图,已知梯形ABCD中,AD∥BC,AB=AC,E是边BC上的点,且∠AED=∠CAD,DE交AC于点F.
(1)求证:△ABE∽△DAF;
(2)当ACFC=AEEC时,求证:AD=BE.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某学校为初三学生定制校服,对部分学生的服装型号做了调查,结果如下:
型号 | 140 | 150 | 160 | 170 | 180 |
男生 | 11 | 18 | 9 | 7 | 5 |
女生 | 9 | 12 | 18 | 7 | 4 |
下列说法正确的是( )
A.男生服装型号的众数大于女生服装型号的众数
B.男生服装型号的中位数等于女生服装型号的中位数
C.男生服装型号的众数小于女生服装型号的众数
D.男生服装型号的中位数大于女生服装型号的中位数
查看答案和解析>>
科目:初中数学 来源: 题型:
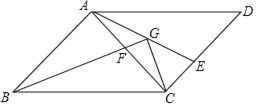
【题目】在平行四边形ABCD中,∠ABC=45°,AB=AC,点E,F分别CD、AC边上的点,且AF=CE,BF的延长线交AE于点G.
(1)若DE=2![]() ,AD=8,求AE.
,AD=8,求AE.
(2)若G是AE的中点,连接CG,求证:![]() AE+CG=BG.
AE+CG=BG.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】春节期间某商场搞促销活动,方案是:在一个不透明的箱子里放4个完全相同的小球,球上分别标“0元”、“20元”、“30元”、“50元”,顾客每消费满300元,就可从箱子里同时摸出两个球,根据这两个小球所标金额之和可获相应价格的礼品;
(1)若某顾客在甲商商场消费320元,至少可得价值______元的礼品,至多可得价值______元的礼品;
(2)请用画树状图或列表的方法,求该顾客去商场消费,获得礼品的总价值不低于50元的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
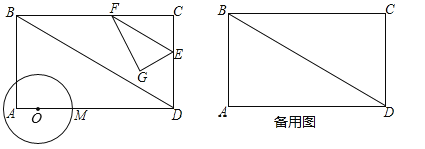
【题目】如图1,已知:在矩形ABCD中,AB![]() cm,AD=9cm,点O从A点出发沿AD以acm/s的速度移向点D移动,以O为圆心,2cm长为半径作圆,交射线AD于M(点M在点O右侧).同时点E从C点出发沿CD以
cm,AD=9cm,点O从A点出发沿AD以acm/s的速度移向点D移动,以O为圆心,2cm长为半径作圆,交射线AD于M(点M在点O右侧).同时点E从C点出发沿CD以![]() cm/s的速度移向点D移动,过E作直线EF∥BD交BC于F,再把△CEF沿着动直线EF对折,点C的对应点为点G. 若在整过移动过程中△EFG的直角顶点G能与点M重合.设运动时间为t(0<t≤3)秒.
cm/s的速度移向点D移动,过E作直线EF∥BD交BC于F,再把△CEF沿着动直线EF对折,点C的对应点为点G. 若在整过移动过程中△EFG的直角顶点G能与点M重合.设运动时间为t(0<t≤3)秒.
(1)求a的值;
(2)在运动过程中,
①当直线FG与⊙O相切时,求t的值;
②是否存在某一时刻t,使点G恰好落在⊙O上(异于点M)?若存在,请直接写出t的值;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
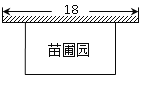
【题目】某课外兴趣活动小组准备围建一个矩形苗圃园,其中一边靠墙,另外三边周长为30米的篱笆围成.已知墙长为18米(如图所示),设这个苗圃园垂直于墙的一边长为x米.
(1)若苗圃园的面积为72平方米,求x;
(2)若平行于墙的一边长不小于8米,这个苗圃园的面积有最大值和最小值吗?如果有,求出最大值和最小值;如果没有,请说明理由;
(3)当这个苗圃园的面积不小于100平方米时,直接写出x的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
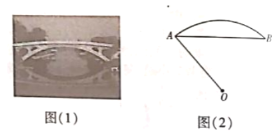
【题目】1400多年前,我国隋代建造的石拱桥——赵州桥(如图(1)),是我国古代人民勤劳与智慧的结晶.如图(2)是它的简化示意图,主桥拱是![]() ,拱高(
,拱高(![]() 的中点到弦
的中点到弦![]() 的距离)为
的距离)为![]() .
.
(1)在图(2)中(点![]() 为圆心),用尺规作图作出
为圆心),用尺规作图作出![]() 的中点
的中点![]() .(不要求写作法,但保留作图痕迹)
.(不要求写作法,但保留作图痕迹)
(2)若![]() ,求主桥拱的跨度
,求主桥拱的跨度![]() 的长.(结果精确到
的长.(结果精确到![]() 参考数据:
参考数据:![]() )
)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com