练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】1400多年前，我国隋代建造的石拱桥——赵州桥(如图(1))，是我国古代人民勤劳与智慧的结晶．如图(2)是它的简化示意图，主桥拱是，拱高(的中点到弦的距离)为．

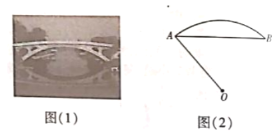
    （1）在图(2)中(点为圆心)，用尺规作图作出的中点．(不要求写作法，但保留作图痕迹)

    （2）若，求主桥拱的跨度的长．(结果精确到参考数据：)

    【答案】（1）见解析；（2）主桥拱的跨度的长为m

    【解析】

    （1）根据垂径定理可以作弦AB的垂直平分线，和弧的交点即是弧的中点；

    （2）根据，设，则AO，表达出CD，求出x的值，根据勾股定理求出AD，进而得到AB的值即可．

    （1）点如图（1）所示．（做法不唯一，正确即可）

    （2）如图（2），设与弦交于点．

    ∵点C为弧AB的中点，

    ∴垂直平分，

    ．

    ∵，

    ∴设，则AO，

    ∴CD=OC-OD=OA-OD=4x-3x=x，

    由题意可知CD=7.2m，即x=7.2，

    答：主桥拱的跨度的长为．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】如图，斜坡AB长10米，按图中的直角坐标系可用表示，点A，B分别在x轴和y轴上，且．在坡上的A处有喷灌设备，喷出的水柱呈抛物线形落到B处，抛物线可用表示．

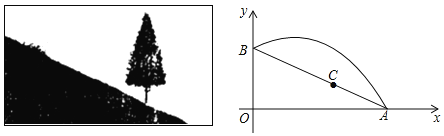
    （1）求抛物线的函数关系式（不必写自变量取值范围）；

    （2）求水柱离坡面AB的最大高度；

    （3）在斜坡上距离A点2米的C处有一颗3.5米高的树，水柱能否越过这棵树？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

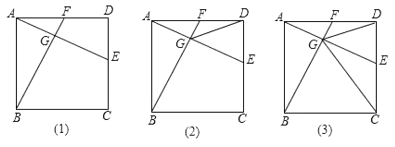
    【题目】如图（1）在正方形中，点是边上一动点，连接，作，重足为，交于.

    （1）求证：；

    （2）连接，若平分，如图（2），求证：点是中点：

    （3）在（2）的条件下，连接，如图（3），求证：.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】若数是关于的不等式组至少有个整数解且所有解都是的解，且使关于的分式有整数解．则满足条件的所有整数的个数是（ ）

    A.B.C.D.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

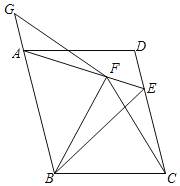
    【题目】在平行四边形ABCD中，以AB为边作等边△ABE，点E在CD上，以BC为边作等边△BCF，点F在AE上，点G在BA延长线上且FG＝FB．

    （1）若CD＝6，AF＝3，求△ABF的面积；

    （2）求证：BE＝AG+CE．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

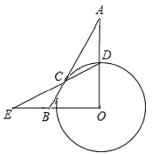
    【题目】如图，Rt△AOB的斜边AB切⊙O于点C，OA交⊙O于点D，连接DC并延长交OB的延长线于点E．已知∠A=∠E，若AB=6，则BC的长为__________．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在边长为1个单位长度的小正方形组成的网格中，已知格点四边形ABCD（顶点是网格线的交点）和格点O．

    （1）将四边形ABCD先向左平移4个单位长度，再向下平移6个单位长度，得到四边形A1B1C1D1，画出平移后的四边形A1B1C1D1，（点A，B，C，D的对应点分别为点A1，B1，C1，D1）；

    （2）将四边形ABCD绕点O逆时针旋转90°，得到四边形A2B2C2D2，画出旋转后的四边形A2B2C2D2（点A、B，C，D的对应点分别为点A2，B2，C2，D2）；

    （3）填空：点C2到A1D1的距离为_______．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】点，分别是的边、延长线上的点，的延长线交于．

    （1）如图1，，，求证：；

    （2）如图2，，，，，求；

    （3）如图3，若，，，求的长．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

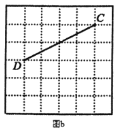
    【题目】图、图分别是的网格，网格中的每个小正方形的边长均为1，点、、、在小正方形的顶点上．请在网格中按要求画出图形：

    （1）在图中画以为斜边的直角三角形（点在小正方形的顶点上），使得；

    （2）在图中画以为边的四边形（点、在小正方形的顶点上），使得四边形是中心对称图形但不是轴对称图形，且，并直接写出四边形的面积．

    查看答案和解析>>

    同步练习册答案