
【题目】点![]() ,
,![]() 分别是
分别是![]() 的边
的边![]() 、
、![]() 延长线上的点,
延长线上的点,![]() 的延长线交
的延长线交![]() 于
于![]() .
.
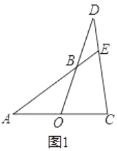
(1)如图1,![]() ,
,![]() ,求证:
,求证:![]() ;
;
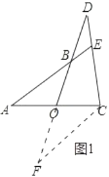
(2)如图2,![]() ,
,![]() ,
,![]() ,
,![]() ,求
,求![]() ;
;
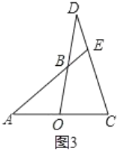
(3)如图3,若![]() ,
,![]() ,
,![]() ,求
,求![]() 的长.
的长.

【答案】(1)详见解析;(2)![]() ;(3)6
;(3)6
【解析】
(1)过C作![]() 交
交![]() 的延长线于
的延长线于![]() ,可以证得
,可以证得![]() ,进而证得
,进而证得![]() ,等角代换得到
,等角代换得到![]() 即可得出结论;
即可得出结论;
(2)如图2中,作![]() 交
交![]() 于
于![]() ,
,![]() 于
于![]() .设
.设![]() ,利用
,利用![]() ,
,![]() ,可知OF是中位线,通过勾股定理求出AE、AF,继而证明
,可知OF是中位线,通过勾股定理求出AE、AF,继而证明![]() ,得出
,得出![]() ,代入数据计算即可得;
,代入数据计算即可得;
(3)过C作![]() 交
交![]() 于
于![]() ,由
,由![]() ,得到
,得到![]() ,计算可得CF=6,利用等角代换可证得CD=CF即可.
,计算可得CF=6,利用等角代换可证得CD=CF即可.
解:(1)如图1中,过C作![]() 交
交![]() 的延长线于
的延长线于![]() ,
,
∵![]() ,
,
∴![]() ,
,![]() ,
,
在![]() 和
和![]() 中,
中,
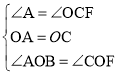 ,
,
∴![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴![]() .
.
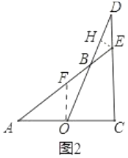
(2)如图2中,作![]() 交
交![]() 于
于![]() ,
,![]() 于
于![]() .设
.设![]() .则
.则![]() ,
,![]() ,
,
∵![]() ,
,![]() ,
,
∴![]() ,
,![]() ,
,
在![]() 中,
中,![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴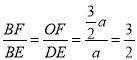 ,
,
∴![]() ,
,
∵![]() ,
,![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴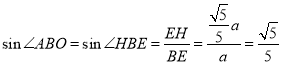 ,
,
故答案为:![]() .
.
(3)如图3中,过C作![]() 交
交![]() 于
于![]() ,
,
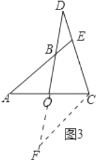
∵![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
故答案为:6.


 小学夺冠AB卷系列答案
小学夺冠AB卷系列答案科目:初中数学 来源: 题型:
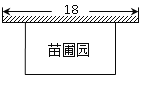
【题目】某课外兴趣活动小组准备围建一个矩形苗圃园,其中一边靠墙,另外三边周长为30米的篱笆围成.已知墙长为18米(如图所示),设这个苗圃园垂直于墙的一边长为x米.
(1)若苗圃园的面积为72平方米,求x;
(2)若平行于墙的一边长不小于8米,这个苗圃园的面积有最大值和最小值吗?如果有,求出最大值和最小值;如果没有,请说明理由;
(3)当这个苗圃园的面积不小于100平方米时,直接写出x的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】1400多年前,我国隋代建造的石拱桥——赵州桥(如图(1)),是我国古代人民勤劳与智慧的结晶.如图(2)是它的简化示意图,主桥拱是![]() ,拱高(
,拱高(![]() 的中点到弦
的中点到弦![]() 的距离)为
的距离)为![]() .
.
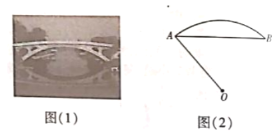
(1)在图(2)中(点![]() 为圆心),用尺规作图作出
为圆心),用尺规作图作出![]() 的中点
的中点![]() .(不要求写作法,但保留作图痕迹)
.(不要求写作法,但保留作图痕迹)
(2)若![]() ,求主桥拱的跨度
,求主桥拱的跨度![]() 的长.(结果精确到
的长.(结果精确到![]() 参考数据:
参考数据:![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在△ABC中,∠ABC=2∠ACB,BD平分∠ABC交AC于点D.
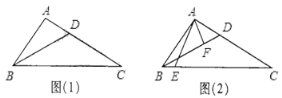
(1)如图(1),若AB=3,AC=5,求AD的长;
(2)如图(2),过点A分别作AC,BD的垂线,分别交BC,BD于点E,F.
①求证:∠ABC=∠EAF;
②求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图在平面直角坐标系中,一次函数![]() 的图象与
的图象与![]() 轴交于点
轴交于点![]() ,与
,与![]() 轴交于点
轴交于点![]() ,二次函数
,二次函数![]() 的图象经过
的图象经过![]() ,
,![]() 两点,且与
两点,且与![]() 轴的负半轴交于点
轴的负半轴交于点![]() ,动点
,动点![]() 在直线
在直线![]() 下方的二次函数图象上.
下方的二次函数图象上.
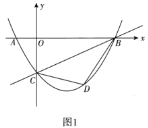
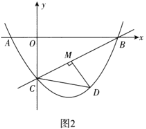
(1)求二次函数的表达式;
(2)如图1,连接![]() ,
,![]() ,设
,设![]() 的面积为
的面积为![]() ,求
,求![]() 的最大值;
的最大值;
(3)如图2,过点![]() 作
作![]() 于点
于点![]() ,是否存在点
,是否存在点![]() ,使得
,使得![]() 中的某个角恰好等于
中的某个角恰好等于![]() 的2倍?若存在,直接写出点
的2倍?若存在,直接写出点![]() 的横坐标;若不存在,请说明理由.
的横坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD中,E、F分别为BC、CD的中点,AF与DE交与点G.则下列结论中:①AF⊥DE;②AD=BG;③GE+GF=![]() GC;④S△AGB=2S四边形ECFG.其中正确的是( )
GC;④S△AGB=2S四边形ECFG.其中正确的是( )
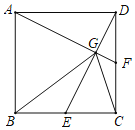
A.1个B.2个C.3个D.4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】抛物线![]() 与
与![]() 轴交于A、B两点,点P在函数
轴交于A、B两点,点P在函数![]() 的图象上,若△PAB为直角三角形,则满足条件的点P的个数为( ).
的图象上,若△PAB为直角三角形,则满足条件的点P的个数为( ).
A. 2个 B. 3个 C. 4个 D. 6个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△BCE中,点A是边BE上一点,以AB为直径的⊙O与CE相切于点D,AD∥OC,点F为OC与⊙O的交点,连接AF.
(1)求证:CB是⊙O的切线;
(2)若∠ECB=60°,AB=6,求图中阴影部分的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在新的教学改革的推动下,某中学初三年级积极推进走班制教学.为了了解一段时间以来“至善班”的学习效果,年级组织了多次定时测试,现随机选取甲、乙两个“至善班”,从中各抽取20名同学在某一次定时测试中的数学成绩,其结果记录如下:
收集数据:
“至善班”甲班的20名同学的数学成绩统计(满分为100分)(单位:分):86 90 60 76 92 83 56 76 85 70 96 96 90 68 78 80 68 96 85 81
“至善班”乙班的20名同学的数学成绩统计(满分为100分)(单位:分):78 96 75 76 82 87 60 54 87 72 100 82 78 86 70 92 76 80 98 78
整理数据:(成绩得分用x表示)
分数 数量 班级 | 0≤x<60 | 60≤x<70 | 70≤x<80 | 80≤x<90 | 90≤x<100 |
甲班(人数) | 1 | 3 | 4 | 6 | 6 |
乙班(人数) | 1 | 1 | 8 | 6 | 4 |
分析数据,并回答下列问题:
(1)完成下表:
平均数 | 中位数 | 众数 | |
甲班 | 80.6 | 82 | a= |
乙班 | 80.35 | b= | 78 |
(2)在“至善班”甲班的扇形图中,成绩在70≤x<80的扇形中,所对的圆心角α的度数为 ,估计全部“至善班”的1600人中优秀人数为 人.(成绩大于等于80分为优秀)
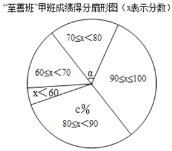
(3)根据以上数据,你认为“至善班” 班(填“甲”或“乙”)所选取做样本的同学的学习效果更好一些,你所做判断的理由是:① ;② .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com