
【题目】抛物线![]() 与
与![]() 轴交于A、B两点,点P在函数
轴交于A、B两点,点P在函数![]() 的图象上,若△PAB为直角三角形,则满足条件的点P的个数为( ).
的图象上,若△PAB为直角三角形,则满足条件的点P的个数为( ).
A. 2个 B. 3个 C. 4个 D. 6个
【答案】D
【解析】分析:先由二次函数与一元二次方程的关系求出A、B两点的坐标,然后分类讨论:①当∠PAB=90°时,则P点的横坐标为-3,根据反比例函数图象上点的坐标特征易得P点有1个;②当∠APB=90°,设P(x,![]() ),根据两点间的距离公式和勾股定理可得(x+3)2+(
),根据两点间的距离公式和勾股定理可得(x+3)2+(![]() )2+(x-3)2+(
)2+(x-3)2+(![]() )2=36,此时P点有4个,③当∠PBA=90°时,P点的横坐标为3,此时P点有1个.
)2=36,此时P点有4个,③当∠PBA=90°时,P点的横坐标为3,此时P点有1个.
详解:解![]() 得,
得,
x=±3,
∴A(-3,0),B(3,0).
①当∠PAB=90°时,如图1,P点的横坐标为-3,把x=-3代入y=![]() 得y=-
得y=-![]() ,所以此时P点有1个;
,所以此时P点有1个;
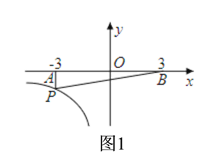
②当∠APB=90°,如图2,设P(x,![]() ),PA2=(x+3)2+(
),PA2=(x+3)2+(![]() )2,PB2=(x-3)2+(
)2,PB2=(x-3)2+(![]() )2,AB2=(3+3)2=36,
)2,AB2=(3+3)2=36,
∵PA2+PB2=AB2,
∴(x+3)2+(![]() )2+(x-3)2+(
)2+(x-3)2+(![]() )2=36,
)2=36,
整理得x4-9x2+4=0,所以x2=![]() ,或x2=
,或x2=![]() ,
,
所以此时P点有4个,
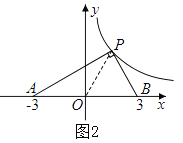
③当∠PBA=90°时,如图3,P点的横坐标为3,把x=3代入y=![]() 得y=
得y=![]() ,所以此时P点有1个;
,所以此时P点有1个;
综上所述,满足条件的P点有6个.
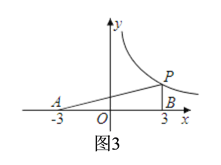
故选:D.


科目:初中数学 来源: 题型:
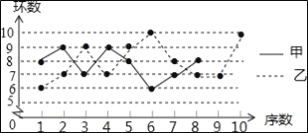
【题目】甲、乙两名射击运动员在某次训练中各射击10发子弹,成绩如表:
甲 | 8 | 9 | 7 | 9 | 8 | 6 | 7 | 8 | 10 | 8 |
乙 | 6 | 7 | 9 | 7 | 9 | 10 | 8 | 7 | 7 | 10 |
且S乙2=1.8,根据上述信息完成下列问题:
(1)将甲运动员的折线统计图补充完整;
(2)乙运动员射击训练成绩的众数是_____,中位数是______.
(3)求甲运动员射击成绩的平均数和方差,并判断甲、乙两人本次射击成绩的稳定性.
查看答案和解析>>
科目:初中数学 来源: 题型:
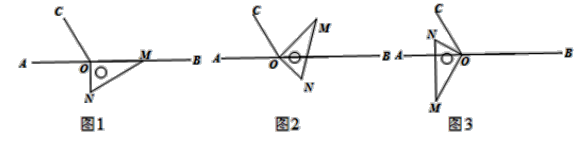
【题目】如图1,点O为直线AB上一点,过点O作射线OC,使∠BOC=120°,将一直角三角板的直角顶点放在点O处,一边OM在射线OB上,另一边ON在直线AB的下方.
(1)如图2,将图1中的三角板绕点O逆时针旋转,使边OM在∠BOC的内部,且OM恰好平分∠BOC.此时∠AOM=_______度;
(2)如图3,继续将图2中的三角板绕点O按逆时针方向旋转,使得ON在∠AOC的内部.探究∠AOM与∠NOC之间数量关系,并说明你的理由;
(3)将图1中的三角板绕点O以每秒10°的速度沿逆时针方向旋转一周,在旋转的过程中,若直线ON恰好平分∠AOC,则此时三角板绕点O旋转的时间是多少秒?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图:在数轴上点A表示数a,点B表示数b,点C表示数c,a是多项式2x24x+1的一次项系数,b是最小的正整数,单项式![]() x2y4的次数为c.
x2y4的次数为c.
![]()
(1)a=___,b=___,c=___;
(2)若将数轴在点B处折叠,则点A与点C___重合(填“能”或“不能”);
(3)点A,B,C开始在数轴上运动,若点C以每秒1个单位长度的速度向右运动,同时,点A和点B分别以每秒3个单位长度和2个单位长度的速度向左运功,t分钟过后,若点A与点B之间的距离表示为AB,点B与点C之间的距离表示为BC,则AB=___,BC=___(用含t的代数式表示);
(4)请问:3ABBC的值是否随着时间t的变化而改变?若变化,请说明理由;若不变,请求其值。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2014年1月,国家发改委出台指导意见,要求2015年底前,所有城市原则上全面实行居民阶梯水价制度. 小军为了解市政府调整水价方案的社会反响,随机访问了自己居住在小区的部分居民,就“每月每户的用水量”和“调价对用水行为改变”两个问题进行调查,并把调查结果整理成下面的图1,图2.
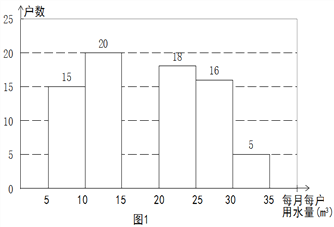
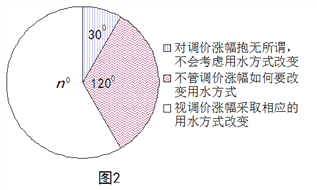
小军发现每月每户的用水量在5m3-35m3之间,有7户居民对用水价格调价涨幅抱无所谓,不用考虑用水方式的改变. 根据小军绘制的图表和发现的信息,完成下列问题:
(1)n =________,小明调查了_____户居民,并补全图1;
(2)每月每户用水量的中位数落在______之间,众数落在_______之间;
(3)如果小明所在的小区有1200户居民,请你估计“视调价涨幅采取相应的用水方式改变”的居民户数有多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:在平面直角坐标系中,边长为8的正方形OABC的两边在坐标轴上(如图).

(1)求点A,B,C的坐标.
(2)经过A,C两点的直线l上有一点P,点D(0,6)在y轴正半轴上,连PD,PB(如图1),若PB2﹣PD2=24,求四边形PBCD的面积.
(3)若点E(0,1),点N(2,0)(如图2),经过(2)问中的点P有一条平行于y轴的直线m,在直线m上是否存在一点M,使得△MNE为直角三角形?若存在,求M点的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我区很多学校开展了大课间活动.某校初三(1)班抽查了10名同学每分钟仰卧起坐的次数,数据如下(单位:次):51,69,64,52,64,72,48,52,76,52.
(1)这组数据的众数为 ______;求这组数据的中位数;
(2)在对初三(2)班10名同学每分钟仰卧起坐次数的抽查中,已知这组数据的平均数正好与初三(1)班上述数据的平均数相同,且除众数(唯一)之外的6个数之和为348.求这组数据的众数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,![]() ,
,![]() 角平分线交BC于O,以OB为半径作⊙O.(1)判定直线AC是否是⊙O的切线,并说明理由;
角平分线交BC于O,以OB为半径作⊙O.(1)判定直线AC是否是⊙O的切线,并说明理由;
(2)连接AO交⊙O于点E,其延长线交⊙O于点D,![]() ,求
,求![]() 的值;
的值;
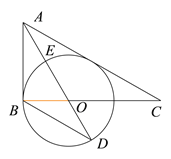
(3)在(2)的条件下,设![]() 的半径为3,求AC的长.
的半径为3,求AC的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
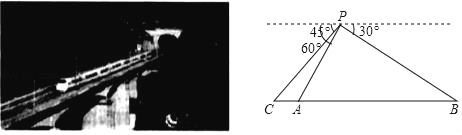
【题目】宜万铁路线上,一列列和谐号动车象一条条巨龙穿梭于恩施崇山峻岭,大多地段桥梁与隧道交替相连如图,勘测队员在山顶P处测得山脚下隧道入口A点处的俯角为60°,隧道出口B点处的俯角为30°,一列动车以180km/h的速度自西向东行驶,当车头抵达入口A点处时,车尾C点处的俯角是45°,整个车身全部进入隧洞恰好用了4s钟时间,求车身完全在隧道中运行的时间(结果精确到1秒,参考数据:![]() ≈1.414,
≈1.414,![]() ≈1.732 ).
≈1.732 ).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com