
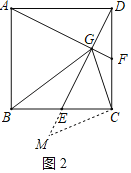
【题目】如图,正方形ABCD中,E、F分别为BC、CD的中点,AF与DE交与点G.则下列结论中:①AF⊥DE;②AD=BG;③GE+GF=![]() GC;④S△AGB=2S四边形ECFG.其中正确的是( )
GC;④S△AGB=2S四边形ECFG.其中正确的是( )
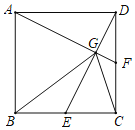
A.1个B.2个C.3个D.4个
【答案】D
【解析】
(1)证△ADF≌△DCE(SAS),∠AFD+∠CDE=90°=∠DGF,AF⊥DE,故①正确;(2)过点B作BH∥DE交AD于H,交AF于K,BH是AG的垂直平分线,BG=AB=AD,故②正确;(3)延长DE至M,使得EM=GF,连接CM,△CEM≌△CFG(SAS),△MCG为等腰直角三角形,故③正确;(4)过G点作TL∥AD,交AB于T,交DC于L,则GL⊥AB,GL⊥DC,证得△DGF∽△DCE,根据相似三角形性质可以求出相应面积关系..
解:
∵正方形ABCD,E,F均为中点
∴AD=BC=DC,EC=DF=$\frac{1}{2}$BC
∵在△ADF和△DCE中,

∴△ADF≌△DCE(SAS)
∴∠AFD=∠DEC
∵∠DEC+∠CDE=90°
∴∠AFD+∠CDE=90°=∠DGF
∴AF⊥DE,故①正确
如图1,过点B作BH∥DE交AD于H,交AF于K
∵AF⊥DE,BH∥DE,E是BC的中点
∴BH⊥AG,H为AD的中点
∴BH是AG的垂直平分线
∴BG=AB=AD,故②正确
如图2
延长DE至M,使得EM=GF,连接CM
∵∠AFD=∠DEC
∴∠CEM=∠CFG
又∵E,F分别为BC,DC的中点
∴CF=CE
∵在△CEM和△CFG中,

∴△CEM≌△CFG(SAS)
∴CM=CG,∠ECM=∠GCF
∵∠GCF+∠BCG=90°
∴∠ECM+∠BCG=∠MCG=90°
∴△MCG为等腰直角三角形
∴GM=GE+EM=GE+GF=![]()
故③正确
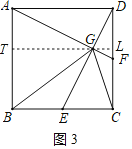
如图3,过G点作TL∥AD,交AB于T,交DC于L,则GL⊥AB,GL⊥DC
设EC=x,则DC=2x,DF=x,由勾股定理得DE ![]()
由DE⊥GF,易证得△DGF∽△DCE
∴![]()
∴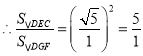
![]() ∴S四边形ECFG=S△DEC﹣
∴S四边形ECFG=S△DEC﹣![]()
![]()
∴S四边形ECFG=![]() x2,S△DGF=
x2,S△DGF=![]() x2
x2
∵DF=x
∴GL=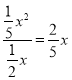
∴TG=![]()
∴S△AGB=![]()
∴S△AGB=2S四边形ECFG
故④正确,
故选D.



 综合自测系列答案
综合自测系列答案科目:初中数学 来源: 题型:
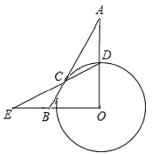
【题目】如图,Rt△AOB的斜边AB切⊙O于点C,OA交⊙O于点D,连接DC并延长交OB的延长线于点E.已知∠A=∠E,若AB=6,则BC的长为__________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2018年湖南省进入高中学习的学生三年后将面对新高考,高考方案与高校招生政策都将有重大变化。某部门为了了解政策的宣传情况,对某初级中学学生进行了随机抽样调查,根据学生对政策的了解程度由高到低分为A,B,C,D四个等级,并对调查结果分析后绘制了如下两幅图不完整的统计图。请你根据图中提供的信息完成下列问题:
(1)求被调查学生的人数,并将条形统计图补充完整;
(2)求扇形统计图中的A等对应的扇形圆心角的度数;
(3)已知该校有1500名学生,估计该校学生对政策内容了解程度达到A等的学生有多少人?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图(1),已知点G在正方形ABCD的对角线AC上,GE⊥BC,垂足为点E,GF⊥CD,垂足为点F.
(1)证明与推断:
①求证:四边形CEGF是正方形;
②推断:![]() 的值为 :
的值为 :
(2)探究与证明:
将正方形CEGF绕点C顺时针方向旋转α角(0°<α<45°),如图(2)所示,试探究线段AG与BE之间的数量关系,并说明理由:
(3)拓展与运用:
正方形CEGF在旋转过程中,当B,E,F三点在一条直线上时,如图(3)所示,延长CG交AD于点H.若AG=6,GH=2![]() ,则BC= .
,则BC= .

查看答案和解析>>
科目:初中数学 来源: 题型:
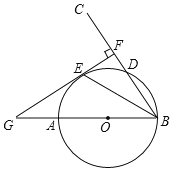
【题目】如图,AB是⊙O的直径,射线BC交⊙O于点D,E是劣弧AD上一点,且![]() =
=![]() ,过点E作EF⊥BC于点F,延长FE和BA的延长线交与点G.
,过点E作EF⊥BC于点F,延长FE和BA的延长线交与点G.
(1)证明:GF是⊙O的切线;
(2)若AG=6,GE=6![]() ,求⊙O的半径.
,求⊙O的半径.
查看答案和解析>>
科目:初中数学 来源: 题型:
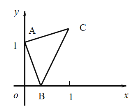
【题目】如右图,点A的坐标为(0,1),点B是x轴正半轴上的一动点,以AB为边作等腰直角△ABC,使∠BAC=90°,如果点B的横坐标为x,点C的纵坐标为y,那么表示y与x的函数关系的图像大致是( )
A.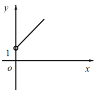 B.
B.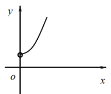
C.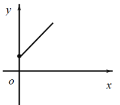 D.
D.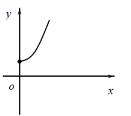
查看答案和解析>>
科目:初中数学 来源: 题型:
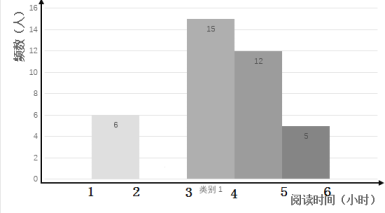
【题目】在开展“经典阅读”活动中,某学校为了解全校学生利用课外时间阅读的情况,学校团委随机抽取若干名学生,调查他们一周的课外阅读时间,并根据调查结果绘制了如下尚不完整的统计表.根据图表信息,解答下列问题:
频率分布表
阅读时间(小时) | 频数(人) | 频率 |
| 6 | 0.12 |
|
| 0.24 |
| 15 | 0.3 |
| 12 |
|
| 5 | 0.1 |
合计 |
| 1 |
(1)求![]() __________,
__________,![]() _________;
_________;
(2)将频数分布直方图补充完整(画图后请标注相应的频数);
(3)在![]() 范围内的5名同学中恰好有2名男生和3名女生,现从中随机挑选2名同学代表学校参加全市经典阅读比赛,请用树状图法或者列表法求出恰好选中“1男1女”的概率.
范围内的5名同学中恰好有2名男生和3名女生,现从中随机挑选2名同学代表学校参加全市经典阅读比赛,请用树状图法或者列表法求出恰好选中“1男1女”的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com