
【题目】2018年湖南省进入高中学习的学生三年后将面对新高考,高考方案与高校招生政策都将有重大变化。某部门为了了解政策的宣传情况,对某初级中学学生进行了随机抽样调查,根据学生对政策的了解程度由高到低分为A,B,C,D四个等级,并对调查结果分析后绘制了如下两幅图不完整的统计图。请你根据图中提供的信息完成下列问题:
(1)求被调查学生的人数,并将条形统计图补充完整;
(2)求扇形统计图中的A等对应的扇形圆心角的度数;
(3)已知该校有1500名学生,估计该校学生对政策内容了解程度达到A等的学生有多少人?

【答案】(1)图见解析;(2)126°;(3)525.
【解析】
(1)利用被调查学生的人数=了解程度达到B等的学生数÷所占比例,即可得出被调查学生的人数,由了解程度达到C等占到的比例可求出了解程度达到C等的学生数,再利用了解程度达到A等的学生数=被调查学生的人数-了解程度达到B等的学生数-了解程度达到C等的学生数-了解程度达到D等的学生数可求出了解程度达到A等的学生数,依此数据即可将条形统计图补充完整;
(2)根据A等对应的扇形圆心角的度数=了解程度达到A等的学生数÷被调查学生的人数×360°,即可求出结论;
(3)利用该校现有学生数×了解程度达到A等的学生所占比例,即可得出结论.
(1)48÷40%=120(人),
120×15%=18(人),
120-48-18-12=42(人).
将条形统计图补充完整,如图所示.
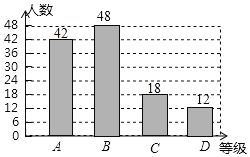
(2)42÷120×100%×360°=126°.
答:扇形统计图中的A等对应的扇形圆心角为126°.
(3)1500×![]() =525(人).
=525(人).
答:该校学生对政策内容了解程度达到A等的学生有525人.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】如图,点P是等边三角形ABC内一点,且PA=3,PB=4, PC=5,若将△APB绕着点B逆时针旋转后得到△CQB,则∠APB的度数______.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,等腰Rt△ABC中,∠ABC=90°,AB=BC,点A,B分别在坐标轴上.
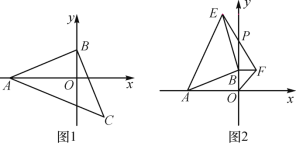
(1)如图1,若点C的横坐标为5,直接写出点B的坐标 ;
(2)如图2,若点A的坐标为(-6,0),点B在y轴的正半轴上运动时,分别以OB,AB为边在第一、第二象限作等腰Rt△OBF,等腰Rt△ABE,连接EF交y轴于点P,当点B在y轴的正半轴上移动时,PB的长度是否发生改变?若不变,求出PB的值;若变化,求PB的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】商场某种新商品每件进价是120元,在试销期间发现,当每件商品售价为130元时,每天可销售70件,当每件商品售价高于130元时,每涨价1元,日销售量就减少1件.据此规律,请回答:
(1)当每件商品售价定为170元时,每天可销售多少件商品?商场获得的日盈利是多少?
(2)在上述条件不变,商品销售正常的情况下,每件商品的销售价定为多少元时,商场日盈利可达到1600元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在直角坐标系![]() 中,直线AB交
中,直线AB交![]() 轴于A(2,0),交
轴于A(2,0),交![]() 轴负半轴于B(0,-10),C为x轴正半轴上一点,且OC=5OA.
轴负半轴于B(0,-10),C为x轴正半轴上一点,且OC=5OA.
(1)求△ABC的面积.
(2)延长BA到P(自己补全图形),使得PA=AB,过点P作PM⊥OC于M,求P点的坐标.
(3)如图,D是第三象限内一动点,直线BE⊥CD于E, OF⊥OD交BE延长线于F.当D点运动时,![]() 的大小是否发生变化?若改变,请说明理由;若不变,求出这个比值.
的大小是否发生变化?若改变,请说明理由;若不变,求出这个比值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某风景区对![]() 个旅游景点的游客人数进行了统计,有关数据如下表:
个旅游景点的游客人数进行了统计,有关数据如下表:
景点 |
|
|
|
|
|
票价(元) |
|
|
|
|
|
平均日人数(千人) |
|
|
|
|
|
![]() 如果这个星期天你去此风景区游玩,小刚、小明也去了,你在哪个景点遇见他们两个的机会较大?为什么?
如果这个星期天你去此风景区游玩,小刚、小明也去了,你在哪个景点遇见他们两个的机会较大?为什么?
![]() 如果到了这个风景区,你不想把这几个景点全部参观完,但又不知选哪一个,于是你想出一个主意:抓阄,那么,你抓出哪种票价的机会较大有多大?此时你参观哪个景点的机会较大?
如果到了这个风景区,你不想把这几个景点全部参观完,但又不知选哪一个,于是你想出一个主意:抓阄,那么,你抓出哪种票价的机会较大有多大?此时你参观哪个景点的机会较大?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将△ABC沿着过AB中点D的直线折叠,使点A落在BC边上的A1,称为第1次操作,折痕DE到BC的距离记为h1;还原纸片后,再将△ADE沿着过AD中点D1的直线折叠,使点A落在DE边上的A2处,称为第2次操作,折痕D1E1到BC的距离记为h2:按上述方法不断操作下去…,经过第2019次操作后得到的折痕D2018E2018,到BC的距离记为h2019:若h1=1,则h2019的值为(____)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点B. F. C.E在一条直线上(点F,C之间不能直接测量),点A,D在直线l的异侧,测得AB=DE,AB∥DE,AC∥DF.
(1)求证:△ABC≌△DEF;
(2)若BE=13m,BF=4m,求FC的长度.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com