
【题目】如图,点P是等边三角形ABC内一点,且PA=3,PB=4, PC=5,若将△APB绕着点B逆时针旋转后得到△CQB,则∠APB的度数______.

【答案】150°
【解析】
首先证明△BPQ为等边三角形,得∠BQP=60°,由△ABP≌CBQ可得QC=PA,在△PQC中,已知三边,用勾股定理逆定理证出得出∠PQC=90°,可求∠BQC的度数,由此即可解决问题.
解:连接PQ,
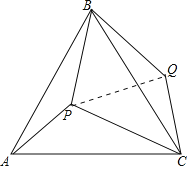
由题意可知△ABP≌△CBQ
则QB=PB=4,PA=QC=3,∠ABP=∠CBQ,
∵△ABC是等边三角形,
∴∠ABC=∠ABP+∠PBC=60°,
∴∠PBQ=∠CBQ+∠PBC=60°,
∴△BPQ为等边三角形,
∴PQ=PB=BQ=4,
又∵PQ=4,PC=5,QC=3,
∴PQ2+QC2=PC2,
∴∠PQC=90°,
∵△BPQ为等边三角形,
∴∠BQP=60°,
∴∠BQC=∠BQP+∠PQC=150°
∴∠APB=∠BQC=150°


 黄冈海淀全程培优测试卷系列答案
黄冈海淀全程培优测试卷系列答案科目:初中数学 来源: 题型:
【题目】已知:如图,在平面直角坐标系中,正比例函数![]() 图像与反比例函数
图像与反比例函数![]() 交于点A(4,
交于点A(4, ![]() ),过点A作
),过点A作![]() 的垂线交x轴于点B.
的垂线交x轴于点B.

(1)求反比例函数的解析式;
(2)如果点C在![]() 的图像上,且△CAB的面积为△OAB面积的2倍,求点C的坐标.
的图像上,且△CAB的面积为△OAB面积的2倍,求点C的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明和小亮进行百米赛跑,小明比小亮跑得快,如果两人同时起跑,小明肯定赢,现在小明让小亮先跑若干米,图中![]() ,
,![]() 分别表示两人的路程与小明追赶时间的关系.
分别表示两人的路程与小明追赶时间的关系.

(1)哪条线表示小明的路程与时间之间的关系?
(2)小明让小亮先跑了多少米?
(3)谁将赢得这场比赛?
(4)![]() 对应的一次函数表达式中,一次项系数是多少?它的实际意义是什么?
对应的一次函数表达式中,一次项系数是多少?它的实际意义是什么?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】现代互联网技术的广泛应用,催生了快递行业的高速发展.阜阳市某家快递公司,2017年3月份与5月份完成投递的快递总件数分别为10万件和12.1万件.现假定该公司每月投递的快递总件数的增长率相同.
(1)求该快递公司投递快递总件数的月平均增长率?
(2) 如果平均每人每月最多可投递快递0.6万件,那么该公司现有的21名快递投递业务员能否完成2017年6月份的快递投递任务?如果不能,请问至少需要增加几名业务员?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图![]() ,在
,在![]() 中,
中,![]() 、
、![]() 的平分线相交于点O
的平分线相交于点O
![]() 若
若![]() ,求
,求![]() 的度数;
的度数;
![]() 若
若![]() ,则
,则![]() ______ ;
______ ;
![]() 若
若![]() ,则
,则![]() ______ ;
______ ;
![]() 如图
如图![]() ,在
,在![]() 中的外角平分线相交于点
中的外角平分线相交于点![]() ,
,![]() ,求
,求![]() 的度数;
的度数;
![]() 上面
上面![]() ,
,![]() 两题中的
两题中的![]() 与
与![]() 有怎样的数量关系?
有怎样的数量关系?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】先化简,再求值
(1)(a2b﹣2ab2﹣b3)÷b﹣(a+b)(a﹣b),其中a=![]() ,b=﹣1.
,b=﹣1.
(2)6x2﹣(2x﹣1)(3x﹣2)+(x+2)(x﹣2),其中x=3.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2018年湖南省进入高中学习的学生三年后将面对新高考,高考方案与高校招生政策都将有重大变化。某部门为了了解政策的宣传情况,对某初级中学学生进行了随机抽样调查,根据学生对政策的了解程度由高到低分为A,B,C,D四个等级,并对调查结果分析后绘制了如下两幅图不完整的统计图。请你根据图中提供的信息完成下列问题:
(1)求被调查学生的人数,并将条形统计图补充完整;
(2)求扇形统计图中的A等对应的扇形圆心角的度数;
(3)已知该校有1500名学生,估计该校学生对政策内容了解程度达到A等的学生有多少人?

查看答案和解析>>
科目:初中数学 来源: 题型:
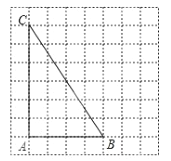
【题目】作图题:如图所示是每一个小方格都是边长为1的正方形网格,
(1)利用网格线作图:
①在![]() 上找一点P,使点P到
上找一点P,使点P到![]() 和
和![]() 的距离相等;
的距离相等;
②在射线![]() 上找一点Q,使
上找一点Q,使![]() .
.
(2)在(1)中连接![]() 与
与![]() ,试说明
,试说明![]() 是直角三角形.
是直角三角形.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com