
【题目】先化简,再求值
(1)(a2b﹣2ab2﹣b3)÷b﹣(a+b)(a﹣b),其中a=![]() ,b=﹣1.
,b=﹣1.
(2)6x2﹣(2x﹣1)(3x﹣2)+(x+2)(x﹣2),其中x=3.
科目:初中数学 来源: 题型:
【题目】如图,点P是等边三角形ABC内一点,且PA=3,PB=4, PC=5,若将△APB绕着点B逆时针旋转后得到△CQB,则∠APB的度数______.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在如图所示的正方形网格中,每个小正方形的边长为1,格点三角形(顶点是网格线的交点的三角形)ABC的顶点A,C的坐标分别为(﹣4,5),(﹣1,3).

(1)在如图所示的网格平面内作出平面直角坐标系;
(2)作出△ABC关于y轴对称的△A′B′C′,并写出点B′的坐标;
(3)P是x轴上的动点,在图中找出使△A′BP周长最短时的点P,直接写出点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,等腰Rt△ABC中,∠ABC=90°,AB=BC,点A,B分别在坐标轴上.
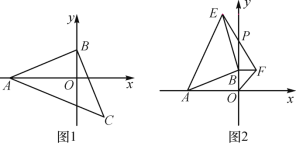
(1)如图1,若点C的横坐标为5,直接写出点B的坐标 ;
(2)如图2,若点A的坐标为(-6,0),点B在y轴的正半轴上运动时,分别以OB,AB为边在第一、第二象限作等腰Rt△OBF,等腰Rt△ABE,连接EF交y轴于点P,当点B在y轴的正半轴上移动时,PB的长度是否发生改变?若不变,求出PB的值;若变化,求PB的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】商场某种新商品每件进价是120元,在试销期间发现,当每件商品售价为130元时,每天可销售70件,当每件商品售价高于130元时,每涨价1元,日销售量就减少1件.据此规律,请回答:
(1)当每件商品售价定为170元时,每天可销售多少件商品?商场获得的日盈利是多少?
(2)在上述条件不变,商品销售正常的情况下,每件商品的销售价定为多少元时,商场日盈利可达到1600元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某风景区对![]() 个旅游景点的游客人数进行了统计,有关数据如下表:
个旅游景点的游客人数进行了统计,有关数据如下表:
景点 |
|
|
|
|
|
票价(元) |
|
|
|
|
|
平均日人数(千人) |
|
|
|
|
|
![]() 如果这个星期天你去此风景区游玩,小刚、小明也去了,你在哪个景点遇见他们两个的机会较大?为什么?
如果这个星期天你去此风景区游玩,小刚、小明也去了,你在哪个景点遇见他们两个的机会较大?为什么?
![]() 如果到了这个风景区,你不想把这几个景点全部参观完,但又不知选哪一个,于是你想出一个主意:抓阄,那么,你抓出哪种票价的机会较大有多大?此时你参观哪个景点的机会较大?
如果到了这个风景区,你不想把这几个景点全部参观完,但又不知选哪一个,于是你想出一个主意:抓阄,那么,你抓出哪种票价的机会较大有多大?此时你参观哪个景点的机会较大?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在△ABC中,∠ACB=90°,AC=BC,直线MN经过点C,且AD⊥MN于D,BE⊥MN于E.
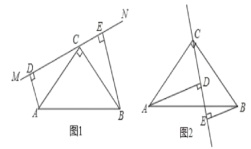
(1)当直线MN绕点C旋转到图1的位置时,△ADC和△CEB全等吗?请说明理由;
(2)聪明的小亮发现,当直线MN绕点C旋转到图1的位置时,可得DE=AD+BE,请你说明其中的理由;
(3)小亮将直线MN绕点C旋转到图2的位置,发现DE、AD、BE之间存在着一个新的数量关系,请直接写出这一数量关系。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com