
【题目】在△ABC中,∠ACB=90°,AC=BC,直线MN经过点C,且AD⊥MN于D,BE⊥MN于E.
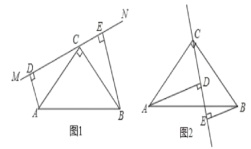
(1)当直线MN绕点C旋转到图1的位置时,△ADC和△CEB全等吗?请说明理由;
(2)聪明的小亮发现,当直线MN绕点C旋转到图1的位置时,可得DE=AD+BE,请你说明其中的理由;
(3)小亮将直线MN绕点C旋转到图2的位置,发现DE、AD、BE之间存在着一个新的数量关系,请直接写出这一数量关系。
【答案】(1)全等,理由见解析;(2)见解析;(3)DE=ADBE.理由见解析
【解析】
(1)根据同角的余角相等得到∠ACD=∠BCE,证明△ADC≌△CEB即可;
(2)根据全等三角形的性质得到BE=CD,CE=AD,结合图形得到结论;
(3)与(1)的证明方法类似,证明△ADC≌△CEB即可.
(1)△ADC≌△CEB.
理由如下:∵∠ACB=90°,
∴∠ACD+∠BCE=90°,
∵BE⊥MN,
∴∠CBE+∠BCE=90°,
∴∠ACD=∠BCE,
在△ADC和△CEB中,
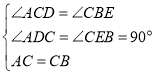 ,
,
∴△ADC≌△CEB;
(2)∵△ADC≌△CEB,
∴BE=CD,CE=AD,
∴DE=CE+CD=AD+BE;
(3)DE=ADBE.
证明:∵∠ACB=90°,
∴∠ACD+∠BCE=90°,
∵AD⊥MN,
∴∠ACD+∠DAC=90°,
∴∠DAC=∠BCE,
在△ADC和△CEB中,
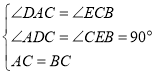 ,
,
∴△ADC≌△CEB,
∴AD=CE,CD=BE,
∴DE=CECD=ADBE.


 同步轻松练习系列答案
同步轻松练习系列答案 课课通课程标准思维方法与能力训练系列答案
课课通课程标准思维方法与能力训练系列答案科目:初中数学 来源: 题型:
【题目】先化简,再求值
(1)(a2b﹣2ab2﹣b3)÷b﹣(a+b)(a﹣b),其中a=![]() ,b=﹣1.
,b=﹣1.
(2)6x2﹣(2x﹣1)(3x﹣2)+(x+2)(x﹣2),其中x=3.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】作图题:如图所示是每一个小方格都是边长为1的正方形网格,
(1)利用网格线作图:
①在![]() 上找一点P,使点P到
上找一点P,使点P到![]() 和
和![]() 的距离相等;
的距离相等;
②在射线![]() 上找一点Q,使
上找一点Q,使![]() .
.
(2)在(1)中连接![]() 与
与![]() ,试说明
,试说明![]() 是直角三角形.
是直角三角形.
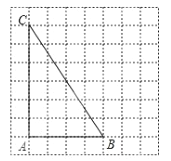
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,AD是BC边上的高,AE、BF分别是∠BAC、∠ABC的平分线,∠BAC=50°,∠ABC=60°,则∠EAD+∠ACD=( )

A. 75° B. 80° C. 85° D. 90°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一次“构造勾股数”的探究性学习中,老师给出了下表:

其中m、n为正整数,且m>n.
(1)观察表格,当m=2,n=1时,此时对应的a、b、c的值能否为直角三角形三边的长?说明你的理由.
(2)探究a,b,c与m、n之间的关系并用含m、n的代数式表示:a=___,b=___,c=___.
(3)以a,b,c为边长的三角形是否一定为直角三角形?如果是,请说明理由;如果不是,请举出反例.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com