
【题目】如图,正方形![]() 的边长为
的边长为![]() ,点
,点![]() 为
为![]() 上任意一点(可以与
上任意一点(可以与![]() 点或
点或![]() 重合),分别过
重合),分别过![]() ,
,![]() ,
,![]() 作射线
作射线![]() 的垂线,垂足分别是
的垂线,垂足分别是![]() ,
,![]() ,
,![]() ,则
,则![]() 的最大值与最小值的和为________.
的最大值与最小值的和为________.

【答案】![]()
【解析】
连接AC,DP,根据正方形的性质可得出AB=CD,S正方形ABCD=1,由三角形的面积公式即可得出![]() ,结合AP的取值范围即可得出BB′+CC′+DD′的范围,将其最大值与最小值相加即可得出结论.
,结合AP的取值范围即可得出BB′+CC′+DD′的范围,将其最大值与最小值相加即可得出结论.
连接AC,DP,如图所示。
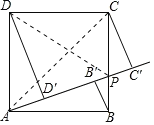
∵四边形ABCD是正方形,正方形ABCD的边长为1,
∴AB=CD,S正方形ABCD=1,
∵S△ADP=![]() S正方形ABCD=
S正方形ABCD=![]() ,S△ABP+S△ACP=S△ABC=
,S△ABP+S△ACP=S△ABC=![]() S正方形ABCD=
S正方形ABCD=![]() ,
,
∴S△ADP+S△ABP+S△ACP=1,
∴![]() APBB′+
APBB′+![]() APCC′+
APCC′+![]() APDD′=
APDD′=![]() AP(BB′+CC′+DD′)=1,
AP(BB′+CC′+DD′)=1,
则![]() ,
,
∵![]()
∴当P与B重合时,有最大值2;当P与C重合时,有最小值![]() .
.
∴![]()
∴BB′+CC′+DD′的最大值与最小值的和为![]() ,.
,.
故答案为:![]()


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】商场某种新商品每件进价是120元,在试销期间发现,当每件商品售价为130元时,每天可销售70件,当每件商品售价高于130元时,每涨价1元,日销售量就减少1件.据此规律,请回答:
(1)当每件商品售价定为170元时,每天可销售多少件商品?商场获得的日盈利是多少?
(2)在上述条件不变,商品销售正常的情况下,每件商品的销售价定为多少元时,商场日盈利可达到1600元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在四边形ABCD中,∠B=∠D=90°,∠BAD=105°,在BC,CD上分别找一点M、N,使得△AMN周长最小,则∠AMN+∠ANM的度数为 ( )

A. 100° B. 105° C. 120° D. 150°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在△ABC中,∠ACB=90°,AC=BC,直线MN经过点C,且AD⊥MN于D,BE⊥MN于E.
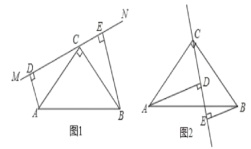
(1)当直线MN绕点C旋转到图1的位置时,△ADC和△CEB全等吗?请说明理由;
(2)聪明的小亮发现,当直线MN绕点C旋转到图1的位置时,可得DE=AD+BE,请你说明其中的理由;
(3)小亮将直线MN绕点C旋转到图2的位置,发现DE、AD、BE之间存在着一个新的数量关系,请直接写出这一数量关系。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点B. F. C.E在一条直线上(点F,C之间不能直接测量),点A,D在直线l的异侧,测得AB=DE,AB∥DE,AC∥DF.
(1)求证:△ABC≌△DEF;
(2)若BE=13m,BF=4m,求FC的长度.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,是用围棋子摆出的图案(用棋子的位置用用有序数对表示,如![]() 点在
点在![]() ),如果再摆一黑一白两枚棋子,使
),如果再摆一黑一白两枚棋子,使![]() 枚棋子组成的图案既是轴对称图形又是中心对称图形,则下列摆放正确的是( )
枚棋子组成的图案既是轴对称图形又是中心对称图形,则下列摆放正确的是( )

A. 黑(3,3),白(3,1) B. 黑(3,1),白(3,3)
C. 黑(1,5),白(5,5) D. 黑(3,2),白(3,3)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形ABCD的对角线AC、BD交于点O,E为AB的中点,G为BC延长线上一点,射线EO与∠ACG的角平分线交于点F,若AB=8,BC=6,则线段EF的长为_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】图1是一辆吊车的实物图,图2是其工作示意图,AC是可以伸缩的起重臂,其转动点A离地面BD的高度AH为3.4m.当起重臂AC长度为9m,张角∠HAC为118°时,求操作平台C离地面的高度(结果保留小数点后一位:参考数据:sin28°≈0.47,cos28°≈0.88,tan28°≈0.53)

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com