
����Ŀ����һ�������카��������̽����ѧϰ�У���ʦ�������±���

����m��n����������m>n.
(1)�۲����m=2��n=1ʱ����ʱ��Ӧ��a��b��c��ֵ�ܷ�Ϊֱ�����������ߵij�?˵��������ɣ�
(2)̽��a��b��c��m��n֮��Ĺ�ϵ���ú�m��n�Ĵ���ʽ��ʾ��a=___��b=___��c=___.
(3)��a��b��cΪ�߳����������Ƿ�һ��Ϊֱ��������?����ǣ���˵�����ɣ�������ǣ���ٳ�����.
���𰸡���1���ܣ����ɼ���������2��m2+n2��2mn��m2-n2����3��һ�������ɼ�����.
��������
��1�������a��b��c��ֵ�����ݹ��ɶ������涨�������жϣ�
��2�����ݸ����������ܽἴ�ɣ�
��3���ֱ�����a2��b2��c2�����ݹ��ɶ������涨�������жϣ�
�⣺��1����m=2��n=1ʱ��a=5��b=4��c=3��
��32+42=52��
��a��b��c��ֵ��Ϊֱ�����������ߵij���
��2���۲�ã�a=m2+n2��b=2mn��c=m2-n2��
��3����a��b��cΪ�߳���������һ��Ϊֱ�������Σ�
��a2=��m2+n2��2=m4+2m2n2+n4��
b2+c2=m4-2m2n2+n4+4m2n2=m4+2m2n2+n4��
��a2=b2+c2��
����a��b��cΪ�߳���������һ��Ϊֱ�������Σ�



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij�羰����![]() �����ξ�����ο�����������ͳ�ƣ��й��������±���
�����ξ�����ο�����������ͳ�ƣ��й��������±���
���� |
|
|
|
|
|
Ʊ�ۣ�Ԫ�� |
|
|
|
|
|
ƽ����������ǧ�ˣ� |
|
|
|
|
|
![]() ��������������ȥ�˷羰�����棬С�ա�С��Ҳȥ�ˣ������ĸ������������������Ļ���ϴ�Ϊʲô��
��������������ȥ�˷羰�����棬С�ա�С��Ҳȥ�ˣ������ĸ������������������Ļ���ϴ�Ϊʲô��
![]() �����������羰�����㲻����⼸������ȫ���ι��꣬���ֲ�֪ѡ��һ�������������һ�����⣺ץ�Σ���ô����ץ������Ʊ�۵Ļ���ϴ��ж��ʱ��ι��ĸ�����Ļ���ϴ�
�����������羰�����㲻����⼸������ȫ���ι��꣬���ֲ�֪ѡ��һ�������������һ�����⣺ץ�Σ���ô����ץ������Ʊ�۵Ļ���ϴ��ж��ʱ��ι��ĸ�����Ļ���ϴ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ڡ�ABC��,��ACB=90����AC=BC��ֱ��MN������C����AD��MN��D��BE��MN��E.
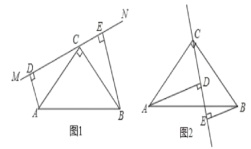
(1)��ֱ��MN�Ƶ�C��ת��ͼ1��λ��ʱ����ADC�͡�CEBȫ����?��˵�����ɣ�
(2)������С�����֣���ֱ��MN�Ƶ�C��ת��ͼ1��λ��ʱ���ɵ�DE=AD+BE������˵�����е����ɣ�
(3)С����ֱ��MN�Ƶ�C��ת��ͼ2��λ�ã�����DE��AD��BE֮�������һ���µ�������ϵ����ֱ��д����һ������ϵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ,��B. F. C.E��һ��ֱ����(��F,C֮�䲻��ֱ�Ӳ���),��A,D��ֱ��l�����,���AB=DE,AB��DE,AC��DF.
(1)��֤����ABC�ա�DEF��
(2)��BE=13m��BF=4m����FC�ij��ȣ�

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������Χ���Ӱڳ���ͼ���������ӵ�λ�������������Ա�ʾ����![]() ����
����![]() ��������ٰ�һ��һ����ö���ӣ�ʹ
��������ٰ�һ��һ����ö���ӣ�ʹ![]() ö������ɵ�ͼ��������Գ�ͼ���������ĶԳ�ͼ�Σ������аڷ���ȷ���ǣ� ��
ö������ɵ�ͼ��������Գ�ͼ���������ĶԳ�ͼ�Σ������аڷ���ȷ���ǣ� ��

A. ��(3,3)����(3,1) B. ��(3,1)����(3,3)
C. ��(1,5)����(5,5) D. ��(3,2)����(3,3)
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����m�Dz�С�ک�1��ʵ��������x�ķ���x2+2��m��2��x+m2��3m+3=0����������ȵ�ʵ����x1��x2��
��1����x12+x22=6����mֵ��
��2����T=![]() ����T��ȡֵ��Χ��
����T��ȡֵ��Χ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������ABCD�ĶԽ���AC��BD���ڵ�O��EΪAB���е㣬GΪBC�ӳ�����һ�㣬����EO���ACG�Ľ�ƽ���߽��ڵ�F����AB=8��BC=6�����߶�EF�ij�Ϊ_____��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ڡ�ABC�У���ACB=90�㣬AC=BC������C�ڡ�ABC����ֱ��MN��AM��MN��M��BN��MN��N��
��1����֤��MN=AM+BN��
��2��������C�ڡ�ABC����ֱ��MN��AM��MN��M��BN��MN��N����AM��BN��MN֮����ʲô��ϵ����˵�����ɣ�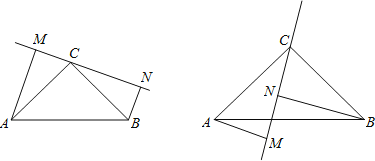
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ�����![]() �У�
�У�![]() ��������һ��P��ʹ��
��������һ��P��ʹ��![]() ��
��![]() �������ס��ҡ������������ֱ����£�
�������ס��ҡ������������ֱ����£�
�ף���BΪԲ�ģ�AB��Ϊ�뾶������AC��P�㣬��P��Ϊ����
�ң��ֱ���B��CΪԲ�ģ�AB��AC��Ϊ�뾶��������P�㣬��P��Ϊ����
������BC�Ĵ�ֱƽ���ߺ�![]() ��ƽ���ߣ����߽���P�㣬��P��Ϊ����
��ƽ���ߣ����߽���P�㣬��P��Ϊ����
���ڼס��ҡ������˵�����������������ȷ����![]() ����
����![]()

A. ���˽���ȷB. �ס�����ȷ���Ҵ���
C. ����ȷ���ҡ�������D. �״����ҡ�����ȷ
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com