
【题目】如图,锐角![]() 中,
中,![]() ,若想找一点P,使得
,若想找一点P,使得![]() 与
与![]() 互补,甲、乙、丙三人作法分别如下:
互补,甲、乙、丙三人作法分别如下:
甲:以B为圆心,AB长为半径画弧交AC于P点,则P即为所求;
乙:分别以B,C为圆心,AB,AC长为半径画弧交于P点,则P即为所求;
丙:作BC的垂直平分线和![]() 的平分线,两线交于P点,则P即为所求.
的平分线,两线交于P点,则P即为所求.
对于甲、乙、丙三人的作法,下列叙述正确的是![]()
![]()

A. 三人皆正确B. 甲、丙正确,乙错误
C. 甲正确,乙、丙错误D. 甲错误,乙、丙正确
科目:初中数学 来源: 题型:
【题目】在一次“构造勾股数”的探究性学习中,老师给出了下表:

其中m、n为正整数,且m>n.
(1)观察表格,当m=2,n=1时,此时对应的a、b、c的值能否为直角三角形三边的长?说明你的理由.
(2)探究a,b,c与m、n之间的关系并用含m、n的代数式表示:a=___,b=___,c=___.
(3)以a,b,c为边长的三角形是否一定为直角三角形?如果是,请说明理由;如果不是,请举出反例.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我们知道,解一元一次方程,可以把它转化为两个一元一次方程来解,其实用“转化”的数学思想,我们还可以解一些新的方程,例如一元三次方程x3+x2﹣2x=0,可以通过因式分解把它转化为x(x2+x﹣2)=0,解方程x=0和x2+x﹣2=0,可得方程x3+x2﹣2x=0的解.
(1)方程x3+x2﹣2x=0的解是x1=0,x2= ,x3= .
(2)用“转化”思想求方程![]() =x的解.
=x的解.
(3)如图,已知矩形草坪ABCD的长AD=14m,宽AB=12m,小华把一根长为28m的绳子的一端固定在点B处,沿草坪边沿BA、AD走到点P处,把长绳PB段拉直并固定在点P处,然后沿草坪边沿PD、DC走到点C处,把长绳剩下的一段拉直,长绳的另一端恰好落在点C处,求AP的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点P是AOB内任意一点,OP=10cm,点P与点![]() 关于射线OA对称,点P与点
关于射线OA对称,点P与点![]() 关于射线OB对称,连接
关于射线OB对称,连接![]() 交OA于点C,交OB于点D,当△PCD的周长是10cm时,∠AOB的度数是______度。
交OA于点C,交OB于点D,当△PCD的周长是10cm时,∠AOB的度数是______度。

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一款名为超级玛丽的游戏中,玛丽到达一个高为10米的高台A,利用旗杆顶部的绳索,划过90°到达与高台A水平距离为17米,高为3米的矮台B,求旗杆的高度OM和玛丽在荡绳索过程中离地面的最低点的高度MN.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在直角△ABC中,∠BAC=90°,AB=3,M是边BC上的点,连接AM.如果将△ABM沿直线AM翻折后,点B恰好在边AC的中点处,那么点M到AC的距离是( )

A. 1.5 B. 2 C. 2.5 D. 3
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,![]() 、
、![]() 两点的坐标分别为
两点的坐标分别为![]() ,
,![]() ,且
,且![]() 满足
满足![]() ,
,![]() 的坐标为
的坐标为![]()
(1)判断![]() 的形状.
的形状.
(2)动点![]() 从点
从点![]() 出发,以
出发,以![]() 个单位/
个单位/![]() 的速度在线段
的速度在线段![]() 上运动,另一动点
上运动,另一动点![]() 从点
从点![]() 出发,以
出发,以![]() 个单位/
个单位/![]() 的速度在射线
的速度在射线![]() 上运动,运动时间为
上运动,运动时间为![]() .
.
①如图2,若![]() ,直线
,直线![]() 交
交![]() 轴于
轴于![]() ,当
,当![]() 时,求
时,求![]() 的值.
的值.
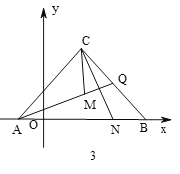
②如图3,若![]() ,当
,当![]() 运动到
运动到![]() 中点时,
中点时,![]() 为
为![]() 上一点,连
上一点,连![]() ,作
,作![]() 交
交![]() 于
于![]() .试探究
.试探究![]() 和
和![]() 的数量关系,并给出证明.
的数量关系,并给出证明.


查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com