Question

【题目】如图1，、两点的坐标分别为，，且满足，的坐标为

（1）判断的形状.

（2）动点从点出发，以个单位/的速度在线段上运动，另一动点从点出发，以个单位/的速度在射线上运动，运动时间为.

①如图2，若，直线交轴于，当时，求的值.

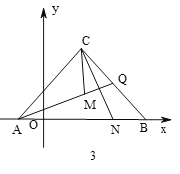
②如图3，若，当运动到中点时，为上一点，连，作交于.试探究和的数量关系，并给出证明.

Answer 1

【答案】（1）为等腰三角形；（2）①6.5s；②AM=CN，证明见解析.

【解析】

（1）作CD⊥AB于D，根据非负数的性质求出a、b的值，根据A、B、C的坐标可得AD=DB，根据线段垂直平分线的性质即可得为等腰三角形；

（2）①作PE∥BC交AB于E，证明△PEH≌△QBH，则PE=BQ，根据等腰三角形及平行线的性质∠PEA=∠PAE，得出PA=BQ，根据线段的相等关系列出关于t的方程，解方程即可；

②延长CM交AB于F，先由点C、M的坐标得出CM⊥AB，根据坐标求出AF=CF=BF，推出∠ACB=90°，可求得∠CAB=∠ABC=∠ACF=45°，证出△BCN≌△CAM即可得出结论.

解：（1）作CD⊥AB于D，

∵，

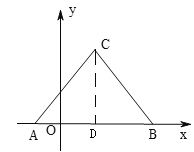
∴a+2=0，b-8=0，

∴a=-2，b=8，

∵的坐标为，

∴OD=3，

∴AD=BD=5，

∴CD为线段AB的垂直平分线，

∴AC=BC，

∴为等腰三角形；

（2）①作PE∥BC交AB于E，

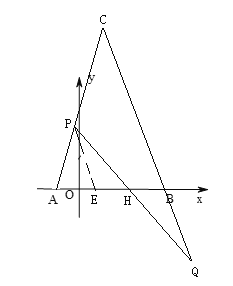
∵PE∥BC，

∴∠EPH=∠BQH，∠PEA=∠ABC，

又∵，∠EHP=∠BHQ，

∴△PEH≌△QBH，

∴PE=BQ，

∵AC=BC，

∴∠CAB=∠ABC，

∴∠CAB=∠PEA，

∴PA=PE，

∴PA=BQ，

由题意得：PA=t，CQ=3t，，

∴t=3t-13，解得：t=6.5s；

②AM=CN

证明：延长CM交AB于F，

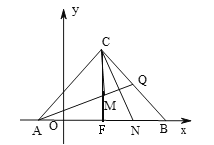
∵C（3,5），

∴CM⊥AB，M（3,0），CF=5，

∵A（-2,0），B（8,0），

∴AF=CF=BF，

∴∠CAF=∠ACF，∠BCF=∠CBF，

∴∠ACB=90°，

∵AC=BC，

∴∠CAB=∠ABC=∠ACF=45°，

∵，∠ACB=90°，

∴∠CQA+∠BCN=∠CQA+∠CAM，

∴∠BCN=∠CAM，

在△BCN和△CAM中

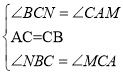
∴△BCN≌△CAM，

∴AM=CN.