【题目】如图，在△ABC中，点O是△ABC内一点，且点O到△ABC三个顶点的距离相等，若∠A＝70°，则∠BOC＝_____________．
【答案】140°
【解析】
连接AO并延长，与BC边交于D，把要求的角分为∠BOC=∠BOD+∠COD通过三角形外角等于不相邻的两个内角之和，转化为∠BOC=∠BAO+∠ABO+∠CAO+∠ACO，根据题意得到∠BAO+∠CAO=70°∠ABO+∠ACO=70°，代入即可求出∠BOC.
解:如图，连接AO并延长，与BC边交于D
∵点O到△ABC三个顶点的距离相等
∴ AO=BO=CO
∴∠BAO=∠ABO, ∠CAO=∠ACO
∵∠BAC=∠BAO+∠CAO=70°∠BOC=∠BOD+∠COD
∴∠ABO+∠ACO=70°
∵ ∠BOC=∠BOD+∠COD
∴∠BOC=∠BOD+∠COD=∠BAO+∠ABO+∠CAO+∠ACO=70°+70°=140°
∴∠BOC=140°
故答案是140°.
小学教材完全解读系列答案科目：初中数学 来源： 题型：
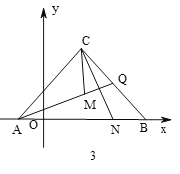
【题目】如图1，
、
两点的坐标分别为
，
，且
满足
，
的坐标为
（1）判断
的形状.
（2）动点
从点出发，以
个单位/
的速度在线段
上运动，另一动点
从点出发，以
个单位/的速度在射线
上运动，运动时间为
.
①如图2，若
，直线
交
轴于
，当
时，求的值.
②如图3，若
，当运动到
中点时，
为
上一点，连
，作
交
于
.试探究
和
的数量关系，并给出证明.
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】已知：如图，在
中，
，
，垂足为点
，
是外角
的平分线，
，垂足为点
，连接
交
于点
．
求证：四边形
为矩形；
当满足什么条件时，四边形是一个正方形？并给出证明．
在的条件下，若
，求正方形周长．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】
已知：如图(1)，在平面直角坐标系中，点
，
，
分别在坐标轴上，且
，
的面积为
，点
从点出发沿
轴负方向以
个单位长度/秒的速度向下运动，连接
，
，点
为
上的中点.
(1)直接写出坐标___________，___________，___________.
(2)设点运动的时间为
秒，问：当
与
垂直且相等时，求此时的值？并说明理由.
(3)如图(2)
，在第四象限内有一动点
，连接
，
，
，点在第四象限内运动，当
，判断是否平分
，并说明理由.
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，在矩形
中，
为
的中点，
过点且
分别交
于
，交
于，点
是
的中点，且
，则下列结论：
；
；
四边形
为菱形；
．其中正确的个数为（ ）
A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
