
【题目】已知:如图,在![]() 中,
中,![]() ,
,![]() ,垂足为点
,垂足为点![]() ,
,![]() 是
是![]() 外角
外角![]() 的平分线,
的平分线,![]() ,垂足为点
,垂足为点![]() ,连接
,连接![]() 交
交![]() 于点
于点![]() .
.

![]() 求证:四边形
求证:四边形![]() 为矩形;
为矩形;
![]() 当
当![]() 满足什么条件时,四边形
满足什么条件时,四边形![]() 是一个正方形?并给出证明.
是一个正方形?并给出证明.
![]() 在
在![]() 的条件下,若
的条件下,若![]() ,求正方形
,求正方形![]() 周长.
周长.
【答案】![]() 证明见解析;(2)
证明见解析;(2)![]() 且
且![]() 时,四边形
时,四边形![]() 是一个正方形;(3)8.
是一个正方形;(3)8.
【解析】
(1)根据已知条件证明∠DAE=90°,已知CE⊥AN,AD⊥BC,根据有三个角是直角的四边形是矩形,可以证明四边形ADCE为矩形;(2)![]() 且
且![]() 时,四边形
时,四边形![]() 是一个正方形,根据添加的条件证明
是一个正方形,根据添加的条件证明![]() ,即可判定四边形ADCE为正方形;(3)根据勾股定理求得AD的长,根据正方形的性质即可求得正方形ADCE周长.
,即可判定四边形ADCE为正方形;(3)根据勾股定理求得AD的长,根据正方形的性质即可求得正方形ADCE周长.
![]() 证明:∵
证明:∵![]() ,
,![]() ,垂足为点
,垂足为点![]() ,
,
∴![]() .
.
∵![]() 是
是![]() 外角
外角![]() 的平分线,
的平分线,
∴![]() .
.
∵![]() 与
与![]() 是邻补角,
是邻补角,
∴![]() ,
,
∴![]() .
.
即∠DAE=90°,
∵![]() ,
,![]() ,
,
∴![]() ,
,
∴四边形![]() 为矩形;
为矩形;
![]() 且
且![]() 时,四边形
时,四边形![]() 是一个正方形,
是一个正方形,
证明:∵![]() 且
且![]() ,
,![]() ,
,
∴![]() ,
,![]() ,
,
∴![]() ,
,
∴![]() .
.
∵四边形![]() 为矩形,
为矩形,
∴四边形![]() 为正方形;
为正方形;
![]() 由勾股定理,得
由勾股定理,得
![]() ,
,![]() ,
,
即![]() ,
,
![]() ,
,
正方形![]() 周长
周长![]() .
.


 能考试期末冲刺卷系列答案
能考试期末冲刺卷系列答案科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠C=90°,∠B=30°,边AB的垂直平分线DE交AB于点E,交BC于点D.CD=3,则BC的长为( )

A. 6 B. 9 C. 6![]() D. 3
D. 3![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在ABCD中,AM,CN分别是∠BAD和∠BCD的平分线,添加一个条件,仍无法判断四边形AMCN为菱形的是( )

A.AM=AN B.MN⊥AC
C.MN是∠AMC的平分线 D.∠BAD=120°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,边长为![]() 的正方形
的正方形![]() 的对角线交于点
的对角线交于点![]() ,把边
,把边![]() 、
、![]() 分别绕点
分别绕点![]() 、
、![]() 同时逆时针旋转
同时逆时针旋转![]() 得四边形
得四边形![]() ,其对角线交点为
,其对角线交点为![]() ,连接
,连接![]() .下列结论:
.下列结论:
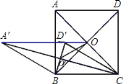
①四边形![]() 为菱形;
为菱形;
②![]() ;
;
③线段![]() 的长为
的长为![]() ;
;
④点![]() 运动到点
运动到点![]() 的路径是线段
的路径是线段![]() .其中正确的结论共有( )
.其中正确的结论共有( )
A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正比例函数y=2x的图象与一次函数y=kx+b的图象交于点A(m,2),一次函数的图象经过点B(2,1).
(1)求一次函数的解析式;
(2)请直接写出不等式组1<kx +b<2x的解集。

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com