Question

【题目】如图，点P是AOB内任意一点，OP=10cm，点P与点关于射线OA对称，点P与点关于射线OB对称，连接交OA于点C，交OB于点D，当△PCD的周长是10cm时，∠AOB的度数是______度。

Answer 1

【答案】30°

【解析】

连接OP1，OP2，据轴对称的性质得出∠P1OA＝∠AOP＝∠P1OP，∠P2OB＝∠POB＝POP2，PC＝CP1，OP＝OP1＝10cm，DP2＝PD，OP＝OP2＝10cm，求出△P1OP2是等边三角形，即可得出答案．

解：如图：连接OP1，OP2，

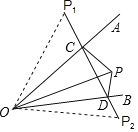
∵点P关于射线OA对称点为点P1

∴OA为PP1的垂直平分线

∴∠P1OA＝∠AOP＝∠P1OP，

∴PC＝CP1，OP＝OP1＝10cm，

同理可得：∠P2OB＝∠POB＝∠POP2，DP2＝PD，OP＝OP2＝10cm，

∴△PCD的周长是＝CD＋PC＋PD＝CD＋CP1＋DP2＝P1 P２＝10cm

∴△P1OP2是等边三角形，

∴∠P1OP2＝60°，

∴∠AOB＝30°，

故答案为：30°