
【题目】如图,已知一条直线过点![]() ,且与抛物线
,且与抛物线![]() 交于
交于![]() ,
,![]() 两点,其中点
两点,其中点![]() 的横坐标是
的横坐标是![]() .
.

![]() 求这条直线的函数关系式及点
求这条直线的函数关系式及点![]() 的坐标.
的坐标.
![]() 在
在![]() 轴上是否存在点
轴上是否存在点![]() ,使得
,使得![]() 是直角三角形?若存在,求出点
是直角三角形?若存在,求出点![]() 的坐标,若不存在,请说明理由.
的坐标,若不存在,请说明理由.
![]() 过线段
过线段![]() 上一点
上一点![]() ,作
,作![]() 轴,交抛物线于点
轴,交抛物线于点![]() ,点
,点![]() 在第一象限,点
在第一象限,点![]() ,当点
,当点![]() 的横坐标为何值时,
的横坐标为何值时,![]() 的长度最大?最大值是多少?
的长度最大?最大值是多少?
【答案】(1) 直线![]() ,B(8,16);(2)存在,
,B(8,16);(2)存在,![]() 或
或![]() ,理由见解析;(3)当
,理由见解析;(3)当![]() 的横坐标为
的横坐标为![]() 时,
时,![]() 的长度的最大值是
的长度的最大值是![]()
【解析】
(1)首先求得点A的坐标,然后利用待定系数法确定直线的解析式,从而求得直线与抛物线的交点坐标;
(2)如图1,过点B作BG∥x轴,过点A作AG∥y轴,交点为G,然后分若∠BAC=90°,则AB2+AC2=BC2;若∠ACB=90°,则AB2=AC2+BC2;若∠ABC=90°,则AB2+BC2=AC2三种情况求得m的值,从而确定点C的坐标;
(3)设M(a,![]() a2),如图2,设MP与y轴交于点Q,首先在Rt△MQN中,由勾股定理得MN=
a2),如图2,设MP与y轴交于点Q,首先在Rt△MQN中,由勾股定理得MN=![]() a2+1,然后根据点P与点M纵坐标相同得到x=
a2+1,然后根据点P与点M纵坐标相同得到x=![]() ,从而得到MN+3PM=-
,从而得到MN+3PM=-![]() a2+3a+9,确定二次函数的最值即可.
a2+3a+9,确定二次函数的最值即可.
解:![]() ∵点
∵点![]() 是直线与抛物线的交点,且横坐标为
是直线与抛物线的交点,且横坐标为![]() ,
,
∴![]() ,
,![]() 点的坐标为
点的坐标为![]() ,
,
设直线的函数关系式为![]() ,
,
将![]() ,
,![]() 代入得
代入得![]() ,
,
解得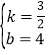 ,
,
∴直线![]() ,
,
∵直线与抛物线相交,
∴![]() ,
,
解得:![]() 或
或![]() ,
,
当![]() 时,
时,![]() ,
,
∴点![]() 的坐标为
的坐标为![]() ;
;
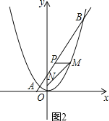
![]() 如图
如图![]() ,过点
,过点![]() 作
作![]() 轴,过点
轴,过点![]() 作
作![]() 轴,交点为
轴,交点为![]() ,
,
∴![]() ,
,
∵由![]() ,
,![]() 可求得
可求得![]() .
.
设点![]() ,同理可得
,同理可得![]() ,
,
![]() ,
,
①若![]() ,则
,则![]() ,即
,即![]() ,
,
解得:![]() ;
;
②若![]() ,则
,则![]() ,即
,即![]() ,
,
解得:![]() 或
或![]() ;
;
③若![]() ,则
,则![]() ,即
,即![]() ,
,
解得:![]() ;
;
∴点![]() 的坐标为
的坐标为![]() ,
,![]() ,
,![]() ,
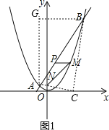
,![]() 设
设![]() ,如图
,如图![]() ,设
,设![]() 与
与![]() 轴交于点
轴交于点![]() ,
,
在![]() 中,由勾股定理得
中,由勾股定理得![]() ,
,
又∵点![]() 与点
与点![]() 纵坐标相同,
纵坐标相同,
∴![]() ,
,
∴![]() ,
,
∴点![]() 的纵坐标为
的纵坐标为![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴当![]() ,
,
又∵![]() ,
,
∴取到最小值![]() ,
,
∴当![]() 的横坐标为
的横坐标为![]() 时,
时,![]() 的长度的最大值是
的长度的最大值是![]() .
.


科目:初中数学 来源: 题型:
【题目】如图,△ABC中,AD是BC边上的高,AE、BF分别是∠BAC、∠ABC的平分线,∠BAC=50°,∠ABC=60°,则∠EAD+∠ACD=( )

A. 75° B. 80° C. 85° D. 90°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,∠MON=30°,点A![]() 、A
、A![]() 、A
、A![]() 、A
、A![]() …在射线ON上,点B
…在射线ON上,点B![]() 、B
、B![]() 、B
、B![]() …在射线OM上,△A
…在射线OM上,△A![]() B
B![]() A
A![]() 、△A
、△A![]() B
B![]() A
A![]() 、△A
、△A![]() B
B![]() A
A![]() …均为等边三角形,若OA
…均为等边三角形,若OA![]() =1,则△A
=1,则△A![]() B
B![]() A
A![]() 的边长为( )
的边长为( )

A.64B.32C.16D.8
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】若![]() ,
,![]() 是一元二次方程
是一元二次方程![]() 的两根,则有
的两根,则有![]() ,
,![]() ,由上式可知,一元二次方程的两根和、两根积是由方程的系数确定的,我们把这个关系称为一元二次方程根与系数的关系.若
,由上式可知,一元二次方程的两根和、两根积是由方程的系数确定的,我们把这个关系称为一元二次方程根与系数的关系.若![]() ,
,![]() 是方程
是方程![]() 的两根,记
的两根,记![]() ,
,![]() ,…,
,…,![]() ,
,
![]() ________;
________;![]() ________;
________;![]() ________;
________;![]() ________;(直接写出结果)
________;(直接写出结果)
![]() 当
当![]() 为不小于
为不小于![]() 的整数时,由
的整数时,由![]() 猜想
猜想![]() ,
,![]() ,
,![]() 有何关系?
有何关系?
![]() 利用
利用![]() 中猜想求
中猜想求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在宽20米,长32米的矩形耕地上,修筑同样宽的三条路(两条纵向,一条横向,并且横向与纵向互相垂直),把这块耕地分成大小相等的六块试验田,要使试验田的面积是570平方米,问道路应该多宽?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点P是AOB内任意一点,OP=10cm,点P与点![]() 关于射线OA对称,点P与点
关于射线OA对称,点P与点![]() 关于射线OB对称,连接
关于射线OB对称,连接![]() 交OA于点C,交OB于点D,当△PCD的周长是10cm时,∠AOB的度数是______度。
交OA于点C,交OB于点D,当△PCD的周长是10cm时,∠AOB的度数是______度。

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某旅行社为吸引市民组团去天水湾风景区旅游,推出如下收费标准:
![]() 如果人数不超过
如果人数不超过![]() 人,人均旅游费用为
人,人均旅游费用为![]() 元;
元;
![]() 如果人数超过
如果人数超过![]() 人,每增加
人,每增加![]() 人,人均旅游费用降低
人,人均旅游费用降低![]() 元,但人均旅游费用不得低于
元,但人均旅游费用不得低于![]() 元.
元.
某单位共付给该旅行社旅游费用![]() 元,问:该单位这次共有多少员工去天水湾风景区旅游?
元,问:该单位这次共有多少员工去天水湾风景区旅游?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com