Question

【题目】已知正方形，点为射线上的一点（不和点、重合），过作，且，过作交射线于．若的面积与四边形的面积之比为，则________．

Answer 1

【答案】或．

【解析】

作EM⊥BA的延长线于点M，延长EF交BC的延长线于点G，易证△PEM≌△PBC，四边形CDEF为平行四边形，则ME=BP=FG=AB+AP，AP=CG．设AB=BC=1，AP=CG=x，用含x的代数式分别表示S△EFC，S四边形PEFC，根据△EFC与四边形PEFC的面积之比为 3：20，列出关于x的方程，解方程求出x的值，然后根据正切函数的定义即可求出tan∠BPC的值．

作EM⊥BA的延长线于点M，延长EF交BC的延长线于点G，

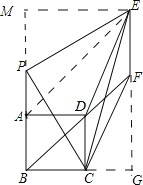
∵PE⊥PC，

∴∠MPE+∠BPC=90°，

∵∠MPE+∠MEP=90°，

∴∠MEP=∠BPC，

在Rt△PBC和Rt△EMP中

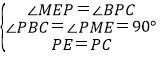
∴Rt△PBC≌Rt△EMP（AAS）

∴PM=BC，ME=PB；

∴PM=AB，

∴PM+PA=AB+PA，

∴MA=ME，

∵MA=ME，AM⊥EM，

∴∠MAE=45°，

∴PB∥EF，

∴四边形ABFE是平行四边形，

∴AB=EF，

∴CD=EF，

∴四边形EFCD是平行四边形，

∴ME=BP=FG=AB+AP，AP=CG，

设AB=BC=1，AP=CG=x，则

S四边形PEFC=S矩形BMEG﹣2S三角形BPC﹣S三角形FCG=（2+x）（1+x）﹣（1+x）﹣（1+x）x= x2+x+1，

S△EFC=x；

∵△EFC与四边形PEFC的面积之比为，

∴x：（x2+x+1）=3：20，

解得x=3或，

∵tan∠BPC=，

∴当x=3时，tan∠BPC=；

当x=时，tan∠BPC=．

tan∠BPC=或．

故答案是：或．