
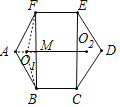
【题目】如图,正六边形ABCDEF的边长是6+4![]() ,点O1,O2分别是△ABF,△CDE的内心,则O1O2=_____.
,点O1,O2分别是△ABF,△CDE的内心,则O1O2=_____.

【答案】9+4![]()
【解析】如图,设△AFB的内切圆的半径为r,过A作AM⊥BF于M,连接O1F、O1A、O1B,解直角三角形求出AM、FM、BM,根据三角形的面积求出r,即可求出答案.
如图,过A作AM⊥BF于M,连接O1F、O1A、O1B,
∵六边形ABCDEF是正六边形,
∴∠A=![]() =120°,AF=AB,
=120°,AF=AB,
∴∠AFB=∠ABF=![]() ×(180°﹣120°)=30°,
×(180°﹣120°)=30°,
∴△AFB边BF上的高AM=![]() AF=
AF=![]() ×(6+4
×(6+4![]() )=3+2
)=3+2![]() ,
,
FM=BM=![]() AM=3
AM=3![]() +6,
+6,
∴BF=3![]() +6+3
+6+3![]() +6=12+6
+6=12+6![]() ,
,
设△AFB的内切圆的半径为r,
∵S△AFB=![]() ,
,
∴![]() ×(3+2
×(3+2![]() )×(3
)×(3![]() +6)
+6)
=![]() ×(6+4
×(6+4![]() )×r+
)×r+![]() ×(6+4
×(6+4![]() )×r+
)×r+![]() ×(12+6
×(12+6![]() )×r,
)×r,
解得:r=![]() ,
,
即O1M=r=![]() ,
,
∴O1O2=2×![]() +6+4
+6+4![]() =9+4
=9+4![]() ,
,
故答案为:9+4![]() .
.


科目:初中数学 来源: 题型:
【题目】定义:如果经过三角形一个顶点的线段把这个三角形分成两个小三角形,其中一个三角形是等腰三角形,另外一个三角形和原三角形的三个内角分别相等,那么这条线段称为原三角形的“和谐分割线”,例如:如图1,等腰直角三角形斜边上的中线就是一条“和谐分割线”
![]() 判断下列两个命题是真命题还是假命题
判断下列两个命题是真命题还是假命题![]() 填“真”或“假”
填“真”或“假”![]()
![]() 等边三角形必存在“和谐分割线”
等边三角形必存在“和谐分割线”
![]() 如果三角形中有一个角是另一个角的两倍,则这个三角形必存在“和谐分割线”.
如果三角形中有一个角是另一个角的两倍,则这个三角形必存在“和谐分割线”.
命题![]() 是______命题,命题
是______命题,命题![]() 是______命题;
是______命题;
![]() 如图2,
如图2,![]() ,
,![]() ,
,![]() ,
,![]() ,试探索
,试探索![]() 是否存在“和谐分割线”?若存在,求出“和谐分割线”的长度;若不存在,请说明理由.
是否存在“和谐分割线”?若存在,求出“和谐分割线”的长度;若不存在,请说明理由.
![]() 如图3,
如图3,![]() 中,
中,![]() ,若线段CD是
,若线段CD是![]() 的“和谐分割线”,且
的“和谐分割线”,且![]() 是等腰三角形,求出所有符合条件的
是等腰三角形,求出所有符合条件的![]() 的度数.
的度数.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某旅行社为吸引市民组团去天水湾风景区旅游,推出如下收费标准:
![]() 如果人数不超过
如果人数不超过![]() 人,人均旅游费用为
人,人均旅游费用为![]() 元;
元;
![]() 如果人数超过
如果人数超过![]() 人,每增加
人,每增加![]() 人,人均旅游费用降低
人,人均旅游费用降低![]() 元,但人均旅游费用不得低于
元,但人均旅游费用不得低于![]() 元.
元.
某单位共付给该旅行社旅游费用![]() 元,问:该单位这次共有多少员工去天水湾风景区旅游?
元,问:该单位这次共有多少员工去天水湾风景区旅游?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,以G(0,1)为圆心,半径为2的圆与x轴交于A、B两点,与y轴交于C,D两点,点E为⊙O上一动点,CF⊥AE于F,则弦AB的长度为________;点E在运动过程中,线段FG的长度的最小值为________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】用适当的方法解下列方程:
(1)4(x-1)2=100
(2)x2-2x-15=0
(3)3x2-13x-10=0
(4)3(x-3)2+x(x-3)=0
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】证明定理:三角形三条边的垂直平分线相交于一点,并且这一点到三个顶点的距离相等,已知:
如图,在△ABC中,分别作AB边、BC边的垂直平分线,两线相交于点P,分别交AB边、BC边于点E、F.
求证:AB、BC、AC的垂直平分线相交于点P
证明:∵点P是AB边垂直平线上的一点,
∴ = ( ).
同理可得,PB= .
∴ = (等量代换).
∴ (到一条线段两个端点距离相等的点,在这条线段的 )
∴AB、BC、AC的垂直平分线 .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com