Question

【题目】如图，在Rt△ABC中，∠ACB＝90°，AB的垂直平分线DE交BC的延长线于F，若∠F＝30°，DE＝1，则EF的长是_____．

Answer 1

【答案】2

【解析】

连接BE，根据垂直平分线的性质、直角三角形的性质，说明∠CBE＝∠F，进一步说明BE＝EF，，然后再根据直角三角形中，30°所对的直角边等于斜边的一半即可.

解：如图：连接BE

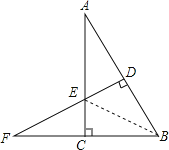
∵AB的垂直平分线DE交BC的延长线于F，

∴AE＝BE，∠A+∠AED＝90°，

∵在Rt△ABC中，∠ACB＝90°，

∴∠F+∠CEF＝90°，

∵∠AED＝∠FEC，

∴∠A＝∠F＝30°，

∴∠ABE＝∠A＝30°，∠ABC＝90°﹣∠A＝60°，

∴∠CBE＝∠ABC﹣∠ABE＝30°，

∴∠CBE＝∠F，

∴BE＝EF，

在Rt△BED中，BE＝2DE＝2×1＝2，

∴EF＝2．

故答案为：2．