
����Ŀ��ij�羰����![]() �����ξ�����ο�����������ͳ�ƣ��й��������±���
�����ξ�����ο�����������ͳ�ƣ��й��������±���
���� |
|
|
|
|
|
Ʊ�ۣ�Ԫ�� |
|
|
|
|
|
ƽ����������ǧ�ˣ� |
|
|
|
|
|
![]() ��������������ȥ�˷羰�����棬С�ա�С��Ҳȥ�ˣ������ĸ������������������Ļ���ϴ�Ϊʲô��
��������������ȥ�˷羰�����棬С�ա�С��Ҳȥ�ˣ������ĸ������������������Ļ���ϴ�Ϊʲô��
![]() �����������羰�����㲻����⼸������ȫ���ι��꣬���ֲ�֪ѡ��һ�������������һ�����⣺ץ�Σ���ô����ץ������Ʊ�۵Ļ���ϴ��ж��ʱ��ι��ĸ�����Ļ���ϴ�
�����������羰�����㲻����⼸������ȫ���ι��꣬���ֲ�֪ѡ��һ�������������һ�����⣺ץ�Σ���ô����ץ������Ʊ�۵Ļ���ϴ��ж��ʱ��ι��ĸ�����Ļ���ϴ�

| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��С����С�����а������ܣ�С����С���ܵÿ죬�������ͬʱ���ܣ�С���϶�Ӯ������С����С�����������ף�ͼ��![]() ��
��![]() �ֱ��ʾ���˵�·����С����ʱ��Ĺ�ϵ.
�ֱ��ʾ���˵�·����С����ʱ��Ĺ�ϵ.

��1�������߱�ʾС����·����ʱ��֮��Ĺ�ϵ��
��2��С����С�������˶����ף�
��3��˭��Ӯ���ⳡ������
��4��![]() ��Ӧ��һ�κ�������ʽ�У�һ����ϵ���Ƕ��٣�����ʵ��������ʲô��
��Ӧ��һ�κ�������ʽ�У�һ����ϵ���Ƕ��٣�����ʵ��������ʲô��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���Ȼ�������ֵ
��1����a2b��2ab2��b3����b����a+b����a��b��������a=![]() ��b=��1��
��b=��1��
��2��6x2����2x��1����3x��2��+��x+2����x��2��������x=3��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��2018�����ʡ�������ѧϰ��ѧ�����������¸߿����߿��������У�������߶������ش�仯��ij����Ϊ���˽����ߵ������������ij������ѧѧ������������������飬����ѧ�������ߵ��˽�̶��ɸߵ��ͷ�ΪA��B��C��D�ĸ��ȼ������Ե������������������������ͼ��������ͳ��ͼ���������ͼ���ṩ����Ϣ����������⣺
��1������ѧ������������������ͳ��ͼ����������
��2��������ͳ��ͼ�е�A�ȶ�Ӧ������Բ�ĽǵĶ�����
��3����֪��У��1500��ѧ�������Ƹ�Уѧ�������������˽�̶ȴﵽA�ȵ�ѧ���ж����ˣ�

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij�д�������ɫ��չģ������������Ծ��ڳ�����������Ҫ��ȾԴ��������ˮ���ؽ�������Ⱦ���ŷţ��ֱ�����������ˮ���д��������³Ƽ����������ؽ�����ת�����������³��ҷ�������������������ˮ��Ⱦָ����ΪQ���ؽ��������ҷ�������һ���������������깤�����ӵ��꿪ʼ����������ÿ�ҹ���һ�꽵�͵�Qֵ����ƽ��ֵn���㣮��һ����40�ҹ������ҷ�����������ʹQֵ������12�������������������ڳ���ˮ�����Ը��ƣ�
��1����n��ֵ��
��2���ӵڶ�����ÿ�����ҷ����������Ĺ�����������һ�궼������ͬ�İٷ���m�����������ҷ��������Ĺ���������190�ң���m��ֵ��������ڶ������ҷ����������Ĺ���������
��3������������ˮ�ü����������ӵڶ�����ÿ����˽��͵�Qֵ����һ�궼���Ӹ���ͬ����ֵa���ڣ�2��������£��ڶ��꣬���ҷ����������Ĺ����ϼƽ��͵�Qֵ�뵱��������������͵�Qֵ��ȣ������꣬�ü���ʹQֵ������39.5�����һ���ü����������͵�Qֵ��a��ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
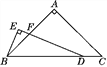
����Ŀ����ͼ����ABC�У�AB��AC����BAC��90�㣬��D���߶�BC�ϣ���EDB��![]() ��C��BE��DE������ΪE��DE��AB�ཻ�ڵ�F.��̽���߶�BE��DF��������ϵ����֤����Ľ��ۣ�
��C��BE��DE������ΪE��DE��AB�ཻ�ڵ�F.��̽���߶�BE��DF��������ϵ����֤����Ľ��ۣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
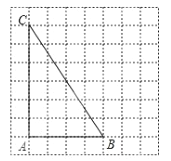
����Ŀ����ͼ�⣺��ͼ��ʾ��ÿһ��С�����DZ߳�Ϊ1������������
(1)������������ͼ��
����![]() ����һ��P��ʹ��P��
����һ��P��ʹ��P��![]() ��
��![]() �ľ�����ȣ�
�ľ�����ȣ�
��������![]() ����һ��Q��ʹ
����һ��Q��ʹ![]() .
.
(2)��(1)������![]() ��
��![]() ����˵��
����˵��![]() ��ֱ��������.
��ֱ��������.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����һ�������카��������̽����ѧϰ�У���ʦ�������±���

����m��n����������m>n.
(1)�۲����m=2��n=1ʱ����ʱ��Ӧ��a��b��c��ֵ�ܷ�Ϊֱ�����������ߵij�?˵��������ɣ�
(2)̽��a��b��c��m��n֮��Ĺ�ϵ���ú�m��n�Ĵ���ʽ��ʾ��a=___��b=___��c=___.
(3)��a��b��cΪ�߳����������Ƿ�һ��Ϊֱ��������?����ǣ���˵�����ɣ�������ǣ���ٳ�����.
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com