
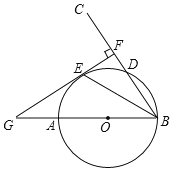
【题目】如图,AB是⊙O的直径,射线BC交⊙O于点D,E是劣弧AD上一点,且![]() =
=![]() ,过点E作EF⊥BC于点F,延长FE和BA的延长线交与点G.
,过点E作EF⊥BC于点F,延长FE和BA的延长线交与点G.
(1)证明:GF是⊙O的切线;
(2)若AG=6,GE=6![]() ,求⊙O的半径.
,求⊙O的半径.
 名校练考卷期末冲刺卷系列答案
名校练考卷期末冲刺卷系列答案科目:初中数学 来源: 题型:
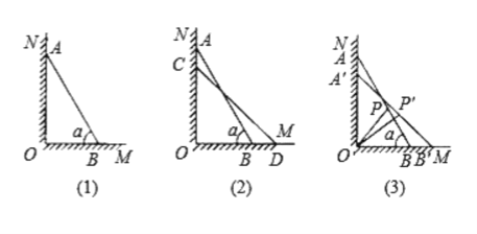
【题目】如图(1)所示,一架长![]() 米的梯子
米的梯子![]() 斜靠在与地面
斜靠在与地面![]() 垂直的墙壁
垂直的墙壁![]() 上,梯子与地面所成的角
上,梯子与地面所成的角![]() 为
为![]() 度.
度.
(1)求图(1)中的![]() 与
与![]() 的长度;
的长度;
(2)若梯子顶端![]() 沿
沿![]() 下滑,同时底端
下滑,同时底端![]() 沿
沿![]() 向右滑行.
向右滑行.
①如图(2)所示,设![]() 点下滑到
点下滑到![]() 点,
点,![]() 点向右滑行到
点向右滑行到![]() 点,并且
点,并且![]() ,请计算
,请计算![]() 的长度;
的长度;
②如图(3)所示,当![]() 点下滑到
点下滑到![]() ,
,![]() 点向右滑行到
点向右滑行到![]() 点时,梯子
点时,梯子![]() 的中点
的中点![]() 也随之运动到
也随之运动到![]() 点,若
点,若![]() ,试求
,试求![]() 的长度.
的长度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在△ABC中,∠ABC=2∠ACB,BD平分∠ABC交AC于点D.
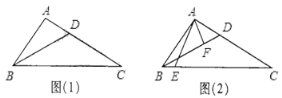
(1)如图(1),若AB=3,AC=5,求AD的长;
(2)如图(2),过点A分别作AC,BD的垂线,分别交BC,BD于点E,F.
①求证:∠ABC=∠EAF;
②求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD中,E、F分别为BC、CD的中点,AF与DE交与点G.则下列结论中:①AF⊥DE;②AD=BG;③GE+GF=![]() GC;④S△AGB=2S四边形ECFG.其中正确的是( )
GC;④S△AGB=2S四边形ECFG.其中正确的是( )
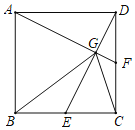
A.1个B.2个C.3个D.4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】抛物线![]() 与
与![]() 轴交于A、B两点,点P在函数
轴交于A、B两点,点P在函数![]() 的图象上,若△PAB为直角三角形,则满足条件的点P的个数为( ).
的图象上,若△PAB为直角三角形,则满足条件的点P的个数为( ).
A. 2个 B. 3个 C. 4个 D. 6个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,以圆O为圆心,半径为1的弧交坐标轴于A,B两点,P是弧![]() 上一点(不与A,B重合),连接OP,设∠POB=α,则点P的坐标是
上一点(不与A,B重合),连接OP,设∠POB=α,则点P的坐标是
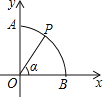
A. (sinα,sinα) B. (cosα,cosα) C. (cosα,sinα) D. (sinα,cosα)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△BCE中,点A是边BE上一点,以AB为直径的⊙O与CE相切于点D,AD∥OC,点F为OC与⊙O的交点,连接AF.
(1)求证:CB是⊙O的切线;
(2)若∠ECB=60°,AB=6,求图中阴影部分的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
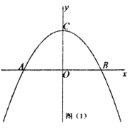
【题目】如图,抛物线![]() 交
交![]() 轴于
轴于![]() 、
、![]() (
(![]() 左
左![]() 右)两点,交
右)两点,交![]() 轴于点
轴于点![]() ,且
,且![]() .
.
(1)如图(1)求抛物线的解析式;
(2)如图(2)![]() 为第四象限抛物线上一点,连接
为第四象限抛物线上一点,连接![]() ,将线段
,将线段![]() 沿着
沿着![]() 轴翻折,得到线段
轴翻折,得到线段![]() ,连接
,连接![]() ,设
,设![]() 点的横坐标为
点的横坐标为![]() ,
,![]() 的面积为
的面积为![]() ,求
,求![]() 与
与![]() 的函数关系式;
的函数关系式;
(3)如图(3)在(2)的条件下,![]() 是第一象限抛物线上的一点,
是第一象限抛物线上的一点,![]() 轴交
轴交![]() 的延长线于
的延长线于![]() ,垂足是
,垂足是![]() ,过点
,过点![]() 作
作![]() 轴交
轴交![]() 轴于
轴于![]() 、交直线
、交直线![]() 于点
于点![]() ,连接
,连接![]() ,
,![]() ,求点
,求点![]() 的坐标.
的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
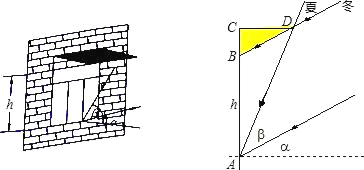
【题目】州政府投资3个亿拟建的恩施民族高中,它位于北纬31°,教学楼窗户朝南,窗户高度为h米,此地一年的冬至这一天的正午时刻太阳光与地面的夹角最小为α,夏至这一天的正午时刻太阳光与地面的夹角最大为β.若你是一名设计师,请你为教学楼的窗户设计一个直角形遮阳蓬BCD,要求它既能最大限度地遮挡夏天炎热的阳光,又能最大限度地使冬天温暖的阳光射入室内(如图).根据测量测得∠α=32.6°,∠β=82.5°,h=2.2米.请你求出直角形遮阳蓬BCD中BC与CD的长各是多少?(结果精确到0.1米)
(参考数据:sin32.6°=0.54,sin82.5°=0.99,tan32.6°=0.64,tan82.5°=7.60)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com