
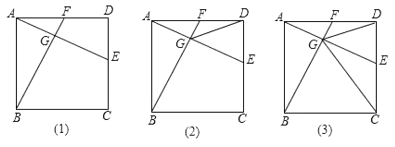
【题目】如图(1)在正方形![]() 中,点
中,点![]() 是
是![]() 边上一动点,连接
边上一动点,连接![]() ,作
,作![]() ,重足为
,重足为![]() ,交
,交![]() 于
于![]() .
.
(1)求证:![]() ;
;
(2)连接![]() ,若
,若![]() 平分
平分![]() ,如图(2),求证:点
,如图(2),求证:点![]() 是
是![]() 中点:
中点:
(3)在(2)的条件下,连接![]() ,如图(3),求证:
,如图(3),求证:![]() .
.
【答案】(1)见解析 (2)见解析 (3)见解析
【解析】
(1)证明△BAF≌△ADE(ASA)即可解决问题;
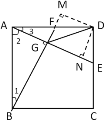
(2) 过点D作DM⊥GF,DN⊥GE,垂足分别为点M、N,先根据AAS证得△BAG≌△AND,推出AG=DN,再由角平分线的性质可知DM=DN,即DM=AG,再证△AFG≌△DFM,推出AF=DF=DE=![]() AD=
AD=![]() CD,即点E是CD的中点 ;
CD,即点E是CD的中点 ;
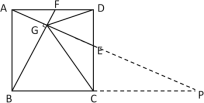
(3)延长AE,BC交于点P,由(2)知DE=CD,证得△ADE≌△PCE,推出AE=PE,再根据中位线判定定理即可得到CB=PC,利用直角三角形斜边中线的性质可证明CG=![]() BP=BC=CP ,即为所证 .
BP=BC=CP ,即为所证 .
(1)证明:在正方形ABCD中,AB=AD,∠BAD=∠D=90o
∴∠2+∠3=90o
又 ∵ BF⊥AE ∴∠1+∠2=90o ∴∠1=∠3
在△BAF与△ADE中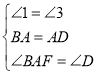
∴ △BAF≌△ADE
∴AF=DE

(2)证明:过点D作DM⊥GF,DN⊥GE,垂足分别为点M、N,
由(1)得∠1=∠3 , ∠BGA=∠AND=90o AB=AD
∴ △BAG≌△ADN ∴AG=DN
又DG平分∠EGF,DM⊥GF,DN⊥GE
∴ DM=DN
∴ DM=AG
又∠AFG=∠DFM , ∠AGF=∠DMF
∴ △AFG≌△DFM
∴AF=DF=DE=![]() AD=
AD=![]() CD
CD
即点E是CD的中点.
(3)延长AE,BC交于点P,由(2)知DE=CE,
∵∠ADE=∠ECP=90o,∠DEA=∠CEP
∴ △ADE≌△PCE
∴AE=PE
又∵CE∥AB ∴ BC=PC
在Rt△BGP中,BC=PC
∴CG=![]() BP=BC
BP=BC
∴CG=CD


科目:初中数学 来源: 题型:
【题目】某学校为初三学生定制校服,对部分学生的服装型号做了调查,结果如下:
型号 | 140 | 150 | 160 | 170 | 180 |
男生 | 11 | 18 | 9 | 7 | 5 |
女生 | 9 | 12 | 18 | 7 | 4 |
下列说法正确的是( )
A.男生服装型号的众数大于女生服装型号的众数
B.男生服装型号的中位数等于女生服装型号的中位数
C.男生服装型号的众数小于女生服装型号的众数
D.男生服装型号的中位数大于女生服装型号的中位数
查看答案和解析>>
科目:初中数学 来源: 题型:
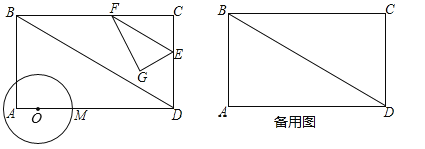
【题目】如图1,已知:在矩形ABCD中,AB![]() cm,AD=9cm,点O从A点出发沿AD以acm/s的速度移向点D移动,以O为圆心,2cm长为半径作圆,交射线AD于M(点M在点O右侧).同时点E从C点出发沿CD以
cm,AD=9cm,点O从A点出发沿AD以acm/s的速度移向点D移动,以O为圆心,2cm长为半径作圆,交射线AD于M(点M在点O右侧).同时点E从C点出发沿CD以![]() cm/s的速度移向点D移动,过E作直线EF∥BD交BC于F,再把△CEF沿着动直线EF对折,点C的对应点为点G. 若在整过移动过程中△EFG的直角顶点G能与点M重合.设运动时间为t(0<t≤3)秒.
cm/s的速度移向点D移动,过E作直线EF∥BD交BC于F,再把△CEF沿着动直线EF对折,点C的对应点为点G. 若在整过移动过程中△EFG的直角顶点G能与点M重合.设运动时间为t(0<t≤3)秒.
(1)求a的值;
(2)在运动过程中,
①当直线FG与⊙O相切时,求t的值;
②是否存在某一时刻t,使点G恰好落在⊙O上(异于点M)?若存在,请直接写出t的值;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
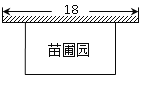
【题目】某课外兴趣活动小组准备围建一个矩形苗圃园,其中一边靠墙,另外三边周长为30米的篱笆围成.已知墙长为18米(如图所示),设这个苗圃园垂直于墙的一边长为x米.
(1)若苗圃园的面积为72平方米,求x;
(2)若平行于墙的一边长不小于8米,这个苗圃园的面积有最大值和最小值吗?如果有,求出最大值和最小值;如果没有,请说明理由;
(3)当这个苗圃园的面积不小于100平方米时,直接写出x的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我们知道,(k+1)2=k2+2k+1,变形得:(k+1)2﹣k2=2k+1,对上面的等式,依次令k=1,2,3,…得:
第1个等式:22﹣12=2×1+1
第2个等式:32﹣22=2×2+1
第3个等式:42﹣32=2×3+1
(1)按规律,写出第n个等式(用含n的等式表示):第n个等式 .
(2)记S1=1+2+3+…+n,将这n个等式两边分别相加,你能求出S1的公式吗?
查看答案和解析>>
科目:初中数学 来源: 题型:
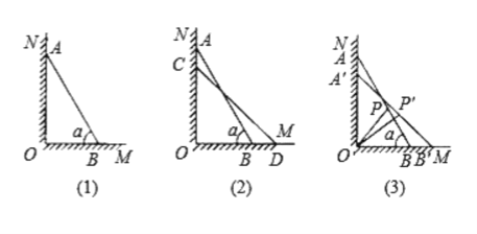
【题目】如图(1)所示,一架长![]() 米的梯子
米的梯子![]() 斜靠在与地面
斜靠在与地面![]() 垂直的墙壁
垂直的墙壁![]() 上,梯子与地面所成的角
上,梯子与地面所成的角![]() 为
为![]() 度.
度.
(1)求图(1)中的![]() 与
与![]() 的长度;
的长度;
(2)若梯子顶端![]() 沿
沿![]() 下滑,同时底端
下滑,同时底端![]() 沿
沿![]() 向右滑行.
向右滑行.
①如图(2)所示,设![]() 点下滑到
点下滑到![]() 点,
点,![]() 点向右滑行到
点向右滑行到![]() 点,并且
点,并且![]() ,请计算
,请计算![]() 的长度;
的长度;
②如图(3)所示,当![]() 点下滑到
点下滑到![]() ,
,![]() 点向右滑行到
点向右滑行到![]() 点时,梯子
点时,梯子![]() 的中点
的中点![]() 也随之运动到
也随之运动到![]() 点,若
点,若![]() ,试求
,试求![]() 的长度.
的长度.
查看答案和解析>>
科目:初中数学 来源: 题型:
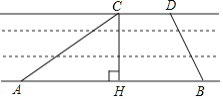
【题目】京杭大运河是世界文化遗产.综合实践活动小组为了测出某段运河的河宽(岸沿是平行的),如图,在岸边分别选定了点A、B和点C、D,先用卷尺量得AB=160m,CD=40m,再用测角仪测得∠CAB=30°,∠DBA=60°,求该段运河的河宽(即CH的长).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】1400多年前,我国隋代建造的石拱桥——赵州桥(如图(1)),是我国古代人民勤劳与智慧的结晶.如图(2)是它的简化示意图,主桥拱是![]() ,拱高(
,拱高(![]() 的中点到弦
的中点到弦![]() 的距离)为
的距离)为![]() .
.
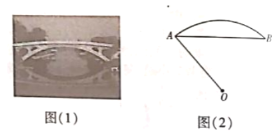
(1)在图(2)中(点![]() 为圆心),用尺规作图作出
为圆心),用尺规作图作出![]() 的中点
的中点![]() .(不要求写作法,但保留作图痕迹)
.(不要求写作法,但保留作图痕迹)
(2)若![]() ,求主桥拱的跨度
,求主桥拱的跨度![]() 的长.(结果精确到
的长.(结果精确到![]() 参考数据:
参考数据:![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】抛物线![]() 与
与![]() 轴交于A、B两点,点P在函数
轴交于A、B两点,点P在函数![]() 的图象上,若△PAB为直角三角形,则满足条件的点P的个数为( ).
的图象上,若△PAB为直角三角形,则满足条件的点P的个数为( ).
A. 2个 B. 3个 C. 4个 D. 6个
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com