
【题目】我们知道,(k+1)2=k2+2k+1,变形得:(k+1)2﹣k2=2k+1,对上面的等式,依次令k=1,2,3,…得:
第1个等式:22﹣12=2×1+1
第2个等式:32﹣22=2×2+1
第3个等式:42﹣32=2×3+1
(1)按规律,写出第n个等式(用含n的等式表示):第n个等式 .
(2)记S1=1+2+3+…+n,将这n个等式两边分别相加,你能求出S1的公式吗?
科目:初中数学 来源: 题型:
【题目】某班男生分成甲、乙两组进行引体向上的专项训练,已知甲组有![]() 名男生,并对两组男生训练前、后引体向上的个数进行统计分析,得到乙组男生训练前、后引体向上的平均个数分别是
名男生,并对两组男生训练前、后引体向上的个数进行统计分析,得到乙组男生训练前、后引体向上的平均个数分别是![]() 个和
个和![]() 个,及下面不完整的统计表和统计图.
个,及下面不完整的统计表和统计图.
甲组男生训练前、后引体向上个数统计表(单位:个)
甲组 | 男生 | 男生 | 男生 | 男生 | 男生 | 男生 | 平均个数 | 众数 | 中位数 |
训练前 |
|
|
|
|
|
|
|
|
|
训练后 |
|
|
|
|
|
|
|
|
|
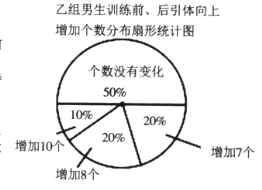
根据以上信息,解答下列问题:
(1)![]() ,
,![]() ,
,![]() ;
;
(2)甲组训练后引体向上的平均个数比训练前增长了 ![]() ;
;
(3)你认为哪组训练效果好?并提供一个支持你观点的理由;
(4)小华说他发现了一个错误:“乙组训练后引体向上个数不变的人数占该组人数的![]() ,所以乙组的平均个数不可能提高
,所以乙组的平均个数不可能提高![]() 个这么多.”你同意他的观点吗?说明理由.
个这么多.”你同意他的观点吗?说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】本学期开学初,学校体育组对九年级某班50名学生进行了跳绳项目的测试,根据测试成绩制作了下面两个统计图.
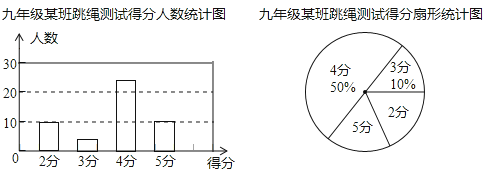
根据统计图解答下列问题:
(1)本次测试的学生中,得4分的学生有多少人?
(2)本次测试的平均分是多少分?
(3)通过一段时间的训练,体育组对该班学生的跳绳项目进行了第二次测试,测得成绩的最低分为3分.且得4分和5分的人数共有45人,平均分比第一次提高了0.8分,问第二次测试中得4分、5分的学生各有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某次数学竞赛中有5道选择题,每题1分,每道题在![]() 、
、![]() 、
、![]() 三个选项中,只有一个是正确的.下表是甲、乙、丙、丁四位同学每道题填涂的答案和这5道题的得分:
三个选项中,只有一个是正确的.下表是甲、乙、丙、丁四位同学每道题填涂的答案和这5道题的得分:
第一题 | 第二题 | 第三题 | 第四题 | 第五题 | 得分 | |
甲 |
|
|
|
|
| 4 |
乙 |
|
|
|
|
| 3 |
丙 |
|
|
|
|
| 2 |
丁 |
|
|
|
|
|
(1)则甲同学错的是第 题;
(2)丁同学的得分是 ;
(3)如果有一个同学得了1分,他的答案可能是 (写出一种即可).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,方格纸中每个小正方形的边长都是1个单位长度,![]() 在平面直角坐标系中的位置如图所示.
在平面直角坐标系中的位置如图所示.
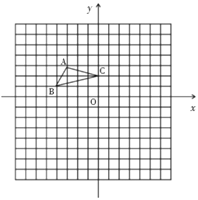
(1)直接写出![]() 关于原点
关于原点![]() 的中心对称图形
的中心对称图形![]() 各顶点坐标:
各顶点坐标:![]() ________
________![]() ________
________![]() ________;
________;
(2)将![]() 绕B点逆时针旋转
绕B点逆时针旋转![]() ,画出旋转后图形
,画出旋转后图形![]() .求
.求![]() 在旋转过程中所扫过的图形的面积和点
在旋转过程中所扫过的图形的面积和点![]() 经过的路径长.
经过的路径长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图(1)在正方形![]() 中,点
中,点![]() 是
是![]() 边上一动点,连接
边上一动点,连接![]() ,作
,作![]() ,重足为
,重足为![]() ,交
,交![]() 于
于![]() .
.
(1)求证:![]() ;
;
(2)连接![]() ,若
,若![]() 平分
平分![]() ,如图(2),求证:点
,如图(2),求证:点![]() 是
是![]() 中点:
中点:
(3)在(2)的条件下,连接![]() ,如图(3),求证:
,如图(3),求证:![]() .
.
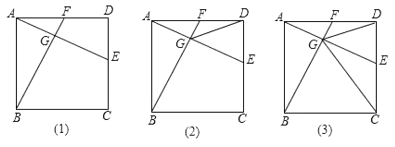
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,给出如下定义:已知两个函数,如果对于任意的自变量![]() ,这两个函数对应的函数值记为
,这两个函数对应的函数值记为![]() , 恒有点
, 恒有点![]() 和点
和点![]() 关于点
关于点![]() 成中心对称(此三个点可以重合),由于对称中心
成中心对称(此三个点可以重合),由于对称中心![]() 都在直线
都在直线![]() 上,所以称这两个函数为关于直线
上,所以称这两个函数为关于直线![]() 的“相依函数”。例如:
的“相依函数”。例如: ![]() 和
和![]() 为关于直线
为关于直线![]() 的 “相依函数”.
的 “相依函数”.
(1)已知点![]() 是直线
是直线![]() 上一点,请求出点
上一点,请求出点![]() 关于点
关于点![]() 成中心对称的点
成中心对称的点![]() 的坐标:
的坐标:
(2)若直线![]() 和它关于直线
和它关于直线![]() 的“相依函数”的图象与
的“相依函数”的图象与![]() 轴围成的三角形的面积为
轴围成的三角形的面积为![]() ,求
,求![]() 的值;
的值;
(3)若二次函数![]() 和
和![]() 为关于直线
为关于直线![]() 的“相依函数”.
的“相依函数”.
①请求出![]() 的值;
的值;
②已知点![]() 、点
、点![]() 连接
连接![]() 直接写出
直接写出![]() 和
和![]() 两条抛物线与线段
两条抛物线与线段![]() 有目只有两个交占时对应的
有目只有两个交占时对应的![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
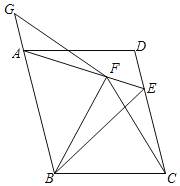
【题目】在平行四边形ABCD中,以AB为边作等边△ABE,点E在CD上,以BC为边作等边△BCF,点F在AE上,点G在BA延长线上且FG=FB.
(1)若CD=6,AF=3,求△ABF的面积;
(2)求证:BE=AG+CE.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“食品安全”受到全社会的广泛关注,育才中学对部分学生就食品安全知识的了解程度,采用随机抽样调查的方式,并根据收集到的信息进行统计,绘制了下面的两幅尚不完整的统计图,请你根据统计图中所提供的信息解答下列问题:
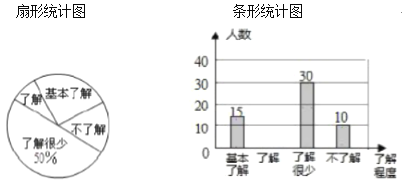
(1)接受问卷调查的学生共有________人,扇形统计图中“基本了解”部分所对应扇形的圆心角为_________![]() ;
;
(2)请补全条形统计图;
(3)若对食品安全知识达到“了解”程度的学生中,男、女生的比例恰为![]() ,现从中随机抽取
,现从中随机抽取![]() 人参加食品安全知识竞赛,则恰好抽到
人参加食品安全知识竞赛,则恰好抽到![]() 个男生和
个男生和![]() 个女生的概率________.
个女生的概率________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com