
【题目】某次数学竞赛中有5道选择题,每题1分,每道题在![]() 、
、![]() 、
、![]() 三个选项中,只有一个是正确的.下表是甲、乙、丙、丁四位同学每道题填涂的答案和这5道题的得分:
三个选项中,只有一个是正确的.下表是甲、乙、丙、丁四位同学每道题填涂的答案和这5道题的得分:
第一题 | 第二题 | 第三题 | 第四题 | 第五题 | 得分 | |
甲 |
|
|
|
|
| 4 |
乙 |
|
|
|
|
| 3 |
丙 |
|
|
|
|
| 2 |
丁 |
|
|
|
|
|
(1)则甲同学错的是第 题;
(2)丁同学的得分是 ;
(3)如果有一个同学得了1分,他的答案可能是 (写出一种即可).
【答案】(1)5;(2)3;(3)A
【解析】
(1)分甲从第1题到第5题依次错一道,进而得出其余四道的正确选项,再根据乙,丙的选项和得分判断,进而得出甲具体选错的题号,即可得出结论;
(2) 分甲从第1题到第5题依次错一道,进而得出其余四道的正确选项,再根据乙丙的选项和得分判断,进而得出甲具体选错的题号,即可得出结论.
(3)由(1)先得出五道题的正确选项,然后留一个正确,其他都错误即可得出结论.
解:(1)当甲选错了第1题,那么,其余四道全对, 针对于乙来看,第1,3,5道错了,做对两道,此时,得分为2,而乙得分3,所以,此种情况不符合题意,
当甲选错了第2题,那么其余四道全对,
针对于乙来看,第2,3,5道错了,做对2道,此时,得分为2分,而乙得分3分,所以,此种情况不符合题意,
当甲选错第3题时,那么其余四道都对,
针对于乙来看,第5道错了,而乙的得分是3分,所以,乙只能做对3道,即:第3题乙也选错,即:第3题的选项C正确,
针对于丙来看,第1题错了,做对4道,此时,丙的得分为4分,而丙的得分为2分,所以此种情况不符合题意,
当甲选错第4题,那么其余四道都对, 针对于乙来看,第3,4,5道错了,做对了2道,此时,得分2分,而乙的得分为3分,所以,此种情况不符合题意,
当甲选错第5题,那么其余四道都对,
针对于乙来看,第3道错了,而乙的得分为3分,所以,乙只能做对3道,所以,乙第5题也错了,所以,第5题的选项A是正确的,
针对于丙来看,第1,3,5题错了,做对了2道,得分2分,
针对于丁来看,第1,3题错了,做对了3道,得分3分,
故答案为5;
(2)当甲选错了第1题,那么,其余四道全对, 针对于乙来看,第1,3,5道错了,做对两道,此时,得分为2,而乙得分3,所以,此种情况不符合题意,
当甲选错了第2题,那么其余四道全对,
针对于乙来看,第2,3,5道错了,做对2道,此时,得分为2分,而乙得分3分,所以,此种情况不符合题意,
当甲选错第3题时,那么其余四道都对,
针对于乙来看,第5道错了,而乙的得分是3分,所以,乙只能做对3道,即:第3题乙也选错,即:第3题的选项C正确,
针对于丙来看,第1题错了,做对4道,此时,丙的得分为4分,而丙的得分为2分,所以,此种情况不符合题意,
当甲选错第4题,那么其余四道都对, 针对于乙来看,第3,4,5道错了,做对了2道,此时,得分2分,而乙的得分为3分,所以,此种情况不符合题意,
当甲选错第5题,那么其余四道都对,
针对于乙来看,第3道错了,而乙的得分为3分,所以,乙只能做对3道,所以,乙第5题也错了,所以,第5题的选项A是正确的,
针对于丙来看,第1,3,5题错了,做对了2道,得分2分,
针对于丁来看,第1,3题错了,做对了3道,得分3分,
故答案为3;
(3)由(1)知,五道题的正确选项分别是:CCABA, 如果有一个同学得了1分,那么,只选对1道, 即:他的答案可能是CACCC或CBCCC或CABAB或BBBBB等,
故答案为:CACCC或BBBBB(答案不唯一).


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】在正方形 ABCD 中, P 为 AB 的中点,![]() 的延长线于点 E ,连接 AE 、 BE ,
的延长线于点 E ,连接 AE 、 BE ,![]() 交 DP 于点 F ,连接 BF 、FC ,下列结论:①
交 DP 于点 F ,连接 BF 、FC ,下列结论:① ![]() ;② FB AB ;③
;② FB AB ;③ ![]() ;④ FC EF . 其中正确的是( )
;④ FC EF . 其中正确的是( )
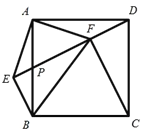
A.①②④B.①③④C.①②③D.①②③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】春节期间某商场搞促销活动,方案是:在一个不透明的箱子里放4个完全相同的小球,球上分别标“0元”、“20元”、“30元”、“50元”,顾客每消费满300元,就可从箱子里同时摸出两个球,根据这两个小球所标金额之和可获相应价格的礼品;
(1)若某顾客在甲商商场消费320元,至少可得价值______元的礼品,至多可得价值______元的礼品;
(2)请用画树状图或列表的方法,求该顾客去商场消费,获得礼品的总价值不低于50元的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
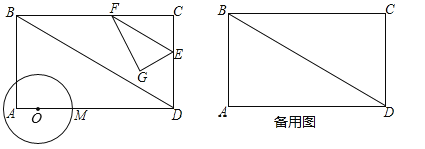
【题目】如图1,已知:在矩形ABCD中,AB![]() cm,AD=9cm,点O从A点出发沿AD以acm/s的速度移向点D移动,以O为圆心,2cm长为半径作圆,交射线AD于M(点M在点O右侧).同时点E从C点出发沿CD以
cm,AD=9cm,点O从A点出发沿AD以acm/s的速度移向点D移动,以O为圆心,2cm长为半径作圆,交射线AD于M(点M在点O右侧).同时点E从C点出发沿CD以![]() cm/s的速度移向点D移动,过E作直线EF∥BD交BC于F,再把△CEF沿着动直线EF对折,点C的对应点为点G. 若在整过移动过程中△EFG的直角顶点G能与点M重合.设运动时间为t(0<t≤3)秒.
cm/s的速度移向点D移动,过E作直线EF∥BD交BC于F,再把△CEF沿着动直线EF对折,点C的对应点为点G. 若在整过移动过程中△EFG的直角顶点G能与点M重合.设运动时间为t(0<t≤3)秒.
(1)求a的值;
(2)在运动过程中,
①当直线FG与⊙O相切时,求t的值;
②是否存在某一时刻t,使点G恰好落在⊙O上(异于点M)?若存在,请直接写出t的值;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知C为线段AB中点,∠ACM=α.Q为线段BC上一动点(不与点B重合),点P在射线CM上,连接PA,PQ,记BQ=kCP.
(1)若α=60°,k=1,
①如图1,当Q为BC中点时,求∠PAC的度数;
②直接写出PA、PQ的数量关系;
(2)如图2,当α=45°时.探究是否存在常数k,使得②中的结论仍成立?若存在,写出k的值并证明;若不存在,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
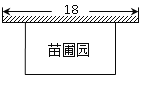
【题目】某课外兴趣活动小组准备围建一个矩形苗圃园,其中一边靠墙,另外三边周长为30米的篱笆围成.已知墙长为18米(如图所示),设这个苗圃园垂直于墙的一边长为x米.
(1)若苗圃园的面积为72平方米,求x;
(2)若平行于墙的一边长不小于8米,这个苗圃园的面积有最大值和最小值吗?如果有,求出最大值和最小值;如果没有,请说明理由;
(3)当这个苗圃园的面积不小于100平方米时,直接写出x的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我们知道,(k+1)2=k2+2k+1,变形得:(k+1)2﹣k2=2k+1,对上面的等式,依次令k=1,2,3,…得:
第1个等式:22﹣12=2×1+1
第2个等式:32﹣22=2×2+1
第3个等式:42﹣32=2×3+1
(1)按规律,写出第n个等式(用含n的等式表示):第n个等式 .
(2)记S1=1+2+3+…+n,将这n个等式两边分别相加,你能求出S1的公式吗?
查看答案和解析>>
科目:初中数学 来源: 题型:
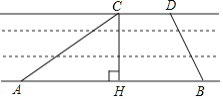
【题目】京杭大运河是世界文化遗产.综合实践活动小组为了测出某段运河的河宽(岸沿是平行的),如图,在岸边分别选定了点A、B和点C、D,先用卷尺量得AB=160m,CD=40m,再用测角仪测得∠CAB=30°,∠DBA=60°,求该段运河的河宽(即CH的长).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图在平面直角坐标系中,一次函数![]() 的图象与
的图象与![]() 轴交于点
轴交于点![]() ,与
,与![]() 轴交于点
轴交于点![]() ,二次函数
,二次函数![]() 的图象经过
的图象经过![]() ,
,![]() 两点,且与
两点,且与![]() 轴的负半轴交于点
轴的负半轴交于点![]() ,动点
,动点![]() 在直线
在直线![]() 下方的二次函数图象上.
下方的二次函数图象上.
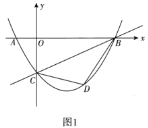
(1)求二次函数的表达式;
(2)如图1,连接![]() ,
,![]() ,设
,设![]() 的面积为
的面积为![]() ,求
,求![]() 的最大值;
的最大值;
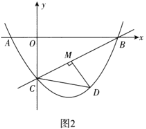
(3)如图2,过点![]() 作
作![]() 于点
于点![]() ,是否存在点
,是否存在点![]() ,使得
,使得![]() 中的某个角恰好等于
中的某个角恰好等于![]() 的2倍?若存在,直接写出点
的2倍?若存在,直接写出点![]() 的横坐标;若不存在,请说明理由.
的横坐标;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com