
【题目】在正方形 ABCD 中, P 为 AB 的中点,![]() 的延长线于点 E ,连接 AE 、 BE ,
的延长线于点 E ,连接 AE 、 BE ,![]() 交 DP 于点 F ,连接 BF 、FC ,下列结论:①
交 DP 于点 F ,连接 BF 、FC ,下列结论:① ![]() ;② FB AB ;③
;② FB AB ;③ ![]() ;④ FC EF . 其中正确的是( )
;④ FC EF . 其中正确的是( )
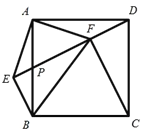
A.①②④B.①③④C.①②③D.①②③④
【答案】D
【解析】
根据已知和正方形的性质推出∠EAB=∠DAF,∠EBA=∠ADP,AB=AD,证△ABE≌△ADF即可;取EF的中点M,连接AM,推出AM=MF=EM=DF,证∠AMB=∠FMB,BM=BM,AM=MF,推出△ABM≌△FBM即可;求出∠FDC=∠EBF,推出△BEF≌△DFC即可.
解:∵正方形ABCD,BE⊥ED,EA⊥FA,
∴AB=AD=CD=BC,∠BAD=∠EAF=90°=∠BEF,
∵∠APD=∠EPB,
∴∠EAB=∠DAF,∠EBA=∠ADP,
∵AB=AD,
∴△ABE≌△ADF,∴①正确;
∴AE=AF,BE=DF,
∴∠AEF=∠AFE=45°,
取EF的中点M,连接AM,
∴AM⊥EF,AM=EM=FM,
∴BE∥AM,
∵AP=BP,
∴AM=BE=DF,
∴∠EMB=∠EBM=45°,
∴∠AMB=90°+45°=135°=∠FMB,
∵BM=BM,AM=MF,
∴△ABM≌△FBM,
∴AB=BF,∴②正确;
∴∠BAM=∠BFM,
∵∠BEF=90°,AM⊥EF,
∴∠BAM+∠APM=90°,∠EBF+∠EFB=90°,
∴∠APF=∠EBF,
∵AB∥CD,
∴∠APD=∠FDC,
∴∠EBF=∠FDC,
∵BE=DF,BF=CD,
∴△BEF≌△DFC,
∴CF=EF,∠DFC=∠FEB=90°,
∴③正确;④正确;

故选D.


科目:初中数学 来源: 题型:
【题目】微信“抢红包”游戏现在受到越来越多的人喜欢,其中有一种玩法“拼手气红包”,用户设置好总金额以及红包个数后,可以随机生成金额不等的红包,现有一用户发了三个“拼手气红包”,总金额为5元,随机被甲、乙、丙三人抢到。
(1)下列事件中,确定事件是__________。
①甲、乙两人抢到的红包金额之和比丙抢到的红包金额多;
②甲抢到的金额为0.5元的红包;
③乙抢到金额为6元的红包。
(2)随机红包分为大、中、小三个金额,用画树状图或列表的方法求出连抽两次最大金额的红包概率。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两车分别从A、B两地同时出发,甲车匀速前往B地,到达B地立即以另一速度按原路匀速返回到A地;乙车匀速前往A地,设甲、乙两车距A地的路程为y(千米),甲车行驶的时间为x(时),y与x之间的函数图象如图所示
(1)求甲车从A地到达B地的行驶时间;
(2)求甲车返回时y与x之间的函数关系式,并写出自变量x的取值范围;
(3)求乙车到达A地时甲车距A地的路程.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,圆柱形玻璃杯高为12cm、底面周长为18cm,在杯内离杯底4cm的点C处有一些蜂蜜,此时一只蚂蚁正好也在杯外壁,离杯上沿4cm与蜂蜜相对的点A处,那么蚂蚁要吃到甜甜的蜂蜜所爬行的最短距离是( )

A.13B.14C.15D.16
查看答案和解析>>
科目:初中数学 来源: 题型:
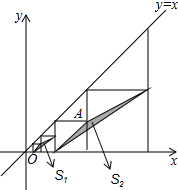
【题目】如图,在平面直角坐标系中,边长不等的正方形依次排列,每个正方形都有一个顶点落在函数![]() 的图象上,从左向右第3个正方形中的一个顶点A的坐标为
的图象上,从左向右第3个正方形中的一个顶点A的坐标为![]() ,阴影三角形部分的面积从左向右依次记为
,阴影三角形部分的面积从左向右依次记为![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() ,则
,则![]() 的值为______
的值为______![]() 用含n的代数式表示,n为正整数
用含n的代数式表示,n为正整数![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
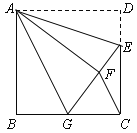
【题目】如图,正方形ABCD中,AB=6,点E在边CD上,且CD=3DE.将△ADE沿AE对折至△AFE,延长EF交边BC于点G,连结AG、CF.
(1)求证:①△ABG≌△AFG; ②BG=GC;
(2)求△FGC的面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com