
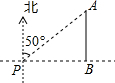 如图,一艘海轮位于灯塔P的北偏东50°方向,距离灯塔P为10海里的点A处,如果海轮沿正南方向航行到灯塔的正东方向B处,那么海轮航行的距离AB的长是( )
如图,一艘海轮位于灯塔P的北偏东50°方向,距离灯塔P为10海里的点A处,如果海轮沿正南方向航行到灯塔的正东方向B处,那么海轮航行的距离AB的长是( )| A. | 10海里 | B. | 10sin50°海里 | C. | 10cos50°海里 | D. | 10tan50°海里 |
 A加金题 系列答案
A加金题 系列答案 全优测试卷系列答案
全优测试卷系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
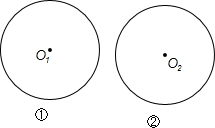 如图,所给两圆的圆心分别为O1,O2,半径都为3,根据要求完成作图(保留作图痕迹,不写作法).
如图,所给两圆的圆心分别为O1,O2,半径都为3,根据要求完成作图(保留作图痕迹,不写作法).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
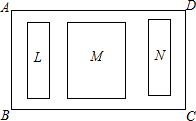 要对一块长60m,宽40m的矩形荒地ABCD(BC>AB)进行绿化和硬化.设计方案如图所示,矩形L、M、N为三块绿地,其余为硬化路面,L、M、N三块绿地周围的硬化路面宽都相等.并使三块绿地面积的和为矩形ABCD面积的$\frac{1}{2}$,求L、M、N三块绿地周围的硬化路面的宽.
要对一块长60m,宽40m的矩形荒地ABCD(BC>AB)进行绿化和硬化.设计方案如图所示,矩形L、M、N为三块绿地,其余为硬化路面,L、M、N三块绿地周围的硬化路面宽都相等.并使三块绿地面积的和为矩形ABCD面积的$\frac{1}{2}$,求L、M、N三块绿地周围的硬化路面的宽.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
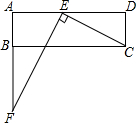 如图,在矩形ABCD中,已知AD>AB,在边AD上取点E,连结CE,过点E作EF⊥CE,与边AB的延长线交于点F.
如图,在矩形ABCD中,已知AD>AB,在边AD上取点E,连结CE,过点E作EF⊥CE,与边AB的延长线交于点F.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com