试题分析:(1)先设⊙O
2运动到E与CD相切,且切点是F;连接EF,并过E作EG∥BC,交CD于G,再过G作GH⊥BC于H,即可得到直角三角形EFG和矩形GEBH.由∠C=60°可得∠CGH=30°,即可得到∠FGE=60°.在Rt△EFG中,根据勾股定理可得EG的值,那么CH=BC-BH=BC-EG.在Rt△CGH中,利用60°的角的正切值可求出GH的值,即可求得结果;
(2)因为0s<t≤3s,所以O
1一定在AD上,连接O
1O
2.利用勾股定理可得到关于t的一元二次方程,解出即可.
(1)如图所示,设点O
2运动到点E处时,⊙O
2与腰CD相切.过点E作EF⊥DC,垂足为F,则EF=4cm.作EG∥BC,交DC于G,作GH⊥BC,垂足为H.

由直角三角形GEF中,∠EGF+∠GEF=90°,
又∠EGF+∠CGH=90°,
∴∠GEF=∠CGH=30°,
设FG=xcm,则EG=2xcm,又EF=4cm,
根据勾股定理得:

,解得

,
则

,
又在直角三角形CHG中,∠C=60°,
∴

则EB=GH=CHtan60°=

∴

秒;
(2)由于0s<t≤3s,所以,点O
1在边AD上.如图连接O
1O
2,则O
1O
2=6cm.

由勾股定理得

,
解得

,

(不合题意,舍去).
答:经过3秒,⊙O
1与⊙O
2外切.
点评:解答本题的关键是注意用含t的代数式来表示线段的长;同时熟记两圆外切时圆心距等于两圆半径的和.

 cm/s的速度向点A运动,⊙O1半径为2cm,⊙O2的半径为4cm,若O1、O2分别从点A、点B同时出发,运动的时间为ts.
cm/s的速度向点A运动,⊙O1半径为2cm,⊙O2的半径为4cm,若O1、O2分别从点A、点B同时出发,运动的时间为ts.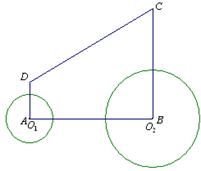
 秒;(2)3秒
秒;(2)3秒
 ,解得
,解得 ,
, ,
,

 秒;
秒;
 ,
, ,
, (不合题意,舍去).
(不合题意,舍去).

 唐印文化课时测评系列答案
唐印文化课时测评系列答案 导学与测试系列答案
导学与测试系列答案

