
【题目】如图所示,抛物线y=ax2+bx+c(a≠0)与x轴交于点A(-2,0)、B(1,0),直线x= ![]() 与此抛物线交于点C,与x轴交于点M,在直线上取点D,使MD=MC,连接AC,BC,AD,BD,某同学根据图象写出下列结论:①a-b=0;②当x<
与此抛物线交于点C,与x轴交于点M,在直线上取点D,使MD=MC,连接AC,BC,AD,BD,某同学根据图象写出下列结论:①a-b=0;②当x< ![]() 时,y随x增大而增大;③四边形ACBD是菱形;④9a-3b+c>0.你认为其中正确的是( )
时,y随x增大而增大;③四边形ACBD是菱形;④9a-3b+c>0.你认为其中正确的是( )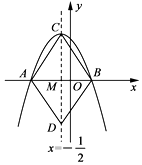
A.②③④
B.①②③
C.①③④
D.①②③④
【答案】B
【解析】(1)∵抛物线y=ax2+bx+c(a≠0)与x轴交于点A(-2,0)、B(1,0),
∴ ![]() ①,
①, ![]() ②,
②,
∴由①-②可得: ![]() ,即:
,即: ![]() ;故第一个结论正确;
;故第一个结论正确;
( 2 )∵点A、B的坐标分别为(-2,0)、(1,0),点M的坐标为(-0.5,0),
∴点M是线段AB的中点,
∴直线 ![]() 是抛物线的对称轴,
是抛物线的对称轴,
又∵抛物线开口向下,
∴当x< ![]() 时,y随x增大而增大,故第二个结论是正确的;
时,y随x增大而增大,故第二个结论是正确的;
( 3 )∵点M既是AB中点,又是CD中点,且CD⊥AB,
∴CD与AB互相垂直平分,
∴四边形ACBD是菱形.故第三个结论是正确的;
( 4 )∵抛物线的开口向下,点A的坐标是(-2,0),
∴结合图象可知:当 ![]() ,
, ![]() ,故第四个结论是错误的;
,故第四个结论是错误的;
综上所述,正确的结论是①②③.
故答案为:B.
①由抛物线与x轴的两交点坐标即可得出抛物线的对称轴为x=-![]() =-0.5,由此即可得出a=b,或将A、B两点坐标分别代入函数解析式,建立方程组,利用加减消元法消去c,即可得出结果,①正确;
=-0.5,由此即可得出a=b,或将A、B两点坐标分别代入函数解析式,建立方程组,利用加减消元法消去c,即可得出结果,①正确;
②根据抛物线的开口向下以及抛物线与x轴的两交点坐标,即可得出当-2<x<1时,y>0,②正确;
③由AB关于x=0.5对称,即可得出AM=BM,再结合MC=MD以及CD⊥AB,得出CD与AB互相垂直平分,即可得出四边形ACBD是菱形,③正确;
④根据当x=-3时,y<0,即可得出9a-3b+c<0,④错误。综上即可得出结论。


科目:初中数学 来源: 题型:
【题目】(1)如图1,AB∥CD,∠A=38°,∠C=50°,求∠APC的度数.(提示:作PE∥AB).
(2)如图2,AB∥DC,当点P在线段BD上运动时,∠BAP=∠α,∠DCP=∠β,求∠CPA与∠α,∠β之间的数量关系,并说明理由.
(3)在(2)的条件下,如果点P在段线OB上运动,请你直接写出∠CPA与∠α,∠β之间的数量关系______.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一次函数y=kx+b的图象与反比例函数y= ![]() 的图象交于A(﹣2,1),B(1,n)两点.
的图象交于A(﹣2,1),B(1,n)两点.
(1)求反比例函数和一次函数的解析式;
(2)根据图象写出使一次函数的值>反比例函数的值的x的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两人从学校出发,沿相同的线路跑向公园.甲先跑一段路程后,乙开始出发,当乙超过甲150米时,乙停在此地等候甲,两人相遇后,乙和甲一起以甲原来的速度继续跑向公园.如图是甲、乙两人在跑步的全过程中经过的路程y(米)与甲出发的时间x(秒)之间函数关系的图象,根据题意填空:
(1)在跑步的全过程中,甲共跑了 米,甲的速度为 米/秒;
(2)乙最早出发时跑步的速度为 米/秒,乙在途中等候甲的时间为 秒;
(3)乙出发 秒后与甲第一次相遇.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】新冠肺炎疫情爆发以来,学生们都在家里上网课,为了了解学生在家上网课使用的设备种类,47中学校初二学年在本学年内随机抽取部分学生进行问卷调查,要求学生在“台式电脑、笔记本电脑、平板电脑、手机、网络电视”五类设备中,选取自己经常使用的一种(必选且只选一种),学年将收集到的调查结果适当整理后,绘制成如图所示的不完整的统计图.请根据图中所给的信息解答下列问题:

(1)在这次调查中,一共抽取了多少名学生?
(2)请通过计算补全条形统计图;
(3)若47中学初二学年共有1000名学生,估计该校初二学年使用手机上课的学生有多少名?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】若顺次连接四边形的各边中点所得的四边形是菱形,则该四边形一定是( )
A. 矩形 B. 一组对边相等,另一组对边平行的四边形
C. 对角线互相垂直的四边形 D. 对角线相等的四边形
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,Rt△ABC中,∠C=90°,AB=5,BC=4,点G为边BC的中点,点D从点C出发沿CA向点A运动,到点A停止,以GD为边作正方形DEFG,则点E运动的路程为_______.

查看答案和解析>>
科目:初中数学 来源: 题型:
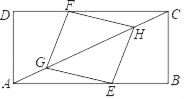
【题目】如图,矩形ABCD中,点E,F分别在边AB与CD上,点G、H在对角线AC上,AG=CH,BE=DF.
(1)求证:四边形EGFH是平行四边形;
(2)若EG=EH,AB=8,BC=4.求AE的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com