练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

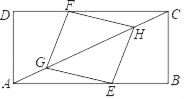
    【题目】如图，矩形ABCD中，点E，F分别在边AB与CD上，点G、H在对角线AC上，AG＝CH，BE＝DF．

    （1）求证：四边形EGFH是平行四边形；

    （2）若EG＝EH，AB＝8，BC＝4．求AE的长．

    【答案】（1）见解析;（2）5.

    【解析】

    （1）依据矩形的性质，即可得出△AEG≌△CFH，进而得到GE=FH，∠CHF=∠AGE，由∠FHG=∠EGH，可得FH∥GE，即可得到四边形EGFH是平行四边形；

    （2）由菱形的性质，即可得到EF垂直平分AC，进而得出AF=CF=AE，设AE=x，则FC=AF=x，DF=8-x，依据Rt△ADF中，AD2+DF2=AF2，即可得到方程，即可得到AE的长．

    （1）证明：

    ,

    ,

    ,

    （2）

    故答案为5.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】如图所示，抛物线y=ax2+bx+c（a≠0）与x轴交于点A（-2，0）、B（1，0），直线x= 与此抛物线交于点C，与x轴交于点M，在直线上取点D，使MD=MC，连接AC，BC，AD，BD，某同学根据图象写出下列结论：①a-b=0；②当x＜ 时，y随x增大而增大；③四边形ACBD是菱形；④9a-3b+c＞0．你认为其中正确的是( )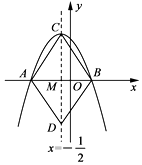

    A.②③④
    B.①②③
    C.①③④
    D.①②③④

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在平面直角坐标系中，直线AB与x轴交于点B，与y轴交于点A，与反比例函数 的图象在第二象限交于点C，CE垂直于x轴，垂足为点E， ，OB=4，OE=2.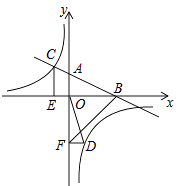

    （1）求反比例函数的解析式；
    （2）若点D是反比例函数图象在第四象限上的点，过点D做DF垂直于y轴，垂足为点F，连接OD、BF，如果 ，求点D的坐标．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】有甲、乙两个不透明的布袋，甲袋中有2个完全相同的小球，分别标有数字0和－2；乙袋中有3个完全相同的小球，分别标有数字－2，0和1，小明从甲袋中随机取出1个小球，记录标有的数字为x，再从乙袋中随机取出1个小球，记录标有的数字为y，这样确定了点Q的坐标(x，y)．
    （1）写出点Q所有可能的坐标；
    （2）求点Q在x轴上的概率．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】原题呈现：若a2+b2+4a﹣2b+5＝0，求a、b的值．

    方法介绍：

    ①看到a2+4a可想到如果添上常数4恰好就是a2+4a+4＝（a+2）2，这个过程叫做“配方”，同理b2﹣2b+1＝（b﹣1）2，恰好把常数5分配完；

    ②从而原式可以化为（a+2）2+（b﹣1）2＝0由平方的非负性可得a+2＝0且b﹣1＝0．

    经验运用：

    （1）若4a2+b2﹣20a+6b+34＝0，求a+b的值．

    （2）若a2+5b2+c2﹣2ab﹣4b+6c+10＝0，求a+b+c的值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】在平面直角坐标系中，点A，B分别是x轴正半轴与y轴正半轴上一点，OA＝m，OB＝n，以AB为边在第一象限内作正方形ABCD．

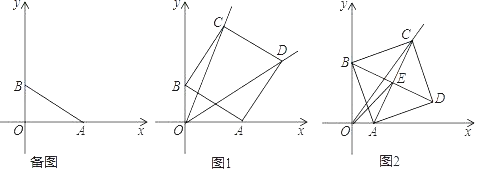
    （1）若m＝4，n＝3，直接写出点C与点D的坐标；

    （2）点C在直线y＝kx（k＞1且k为常数）上运动．

    ①如图1，若k＝2，求直线OD的解析式；

    ②如图2，连接AC、BD交于点E，连接OE，若OE＝2OA，求k的值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】下列各式从左到右的变形，是因式分解的是（）

    A.x2-9+6x=（x+3）（x-3）+6xB.（x+5）（x-2）=x2+3x-10

    C.x2-8x+16=（x-4）2D.x2＋1＝x（x＋）

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】智能折叠电动车是在传统电动车的基础上，根据消费者需求生产的一种新型电动车．某智能折叠电动车公司计划每周生产1400辆，平均每天生产200辆．由于各种原因实际每天生产量与计划每天生产量相比有出入．下表是某周智能折叠电动车生产情况（超计划生产量为正、不足计划生产量为负，单位：辆）

    星期

    一

    二

    三

    四

    五

    六

    七

    生产情况

    （1）根据记录可知前三天共生产智能折叠电动车_______辆；

    （2）产量最多的一天比产量最少的一天多生产________辆；

    （3）若该公司实行按生产的智能折叠电动车数量的多少计工资，即计件工资制．如果每生产一辆智能折叠电动车可得人民币60元，那么该公司工人这一周的工资总额是多少元？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】在“双十二”期间，A，B两个超市开展促销活动，活动方式如下：

    A超市：购物金额打9折后，若超过2000元再优惠300元；

    B超市：购物金额打8折．

    某学校计划购买某品牌的篮球做奖品，该品牌的篮球在A，B两个超市的标价相同．根据商场的活动方式：

    （1）若一次性付款4200元购买这种篮球，则在B商场购买的数量比在A商场购买的数量多5个．请求出这种篮球的标价；

    （2）学校计划购买100个篮球，请你设计一个购买方案，使所需的费用最少．（直接写出方案）

    查看答案和解析>>

    同步练习册答案