
【题目】智能折叠电动车是在传统电动车的基础上,根据消费者需求生产的一种新型电动车.某智能折叠电动车公司计划每周生产1400辆,平均每天生产200辆.由于各种原因实际每天生产量与计划每天生产量相比有出入.下表是某周智能折叠电动车生产情况(超计划生产量为正、不足计划生产量为负,单位:辆)

星期 | 一 | 二 | 三 | 四 | 五 | 六 | 七 |
生产情况 |
|
|
|
|
|
|
|
(1)根据记录可知前三天共生产智能折叠电动车_______辆;
(2)产量最多的一天比产量最少的一天多生产________辆;
(3)若该公司实行按生产的智能折叠电动车数量的多少计工资,即计件工资制.如果每生产一辆智能折叠电动车可得人民币60元,那么该公司工人这一周的工资总额是多少元?
【答案】(1)599辆;(2)26辆;(3)84540元.
【解析】
(1)根据表格中的数据求出前三天生产的总量即可;
(2)求出每天的产量,找出最大比最少的多生产的量即可;
(3)算出一周内总共生产的电动车的数量,然后再乘60,即得到该公司工人这一周的工资总额.
解:(1) “+”表示实际每天比计划每天多生产,“﹣”表示实际每天比计划每天少生产,
故第一天实际生产205辆,
第二天实际生产198辆,
第三天实际生产196辆,
∴前三天共生产智能折叠电动车为:205+198+196=599辆
故答案为:599辆.
(2)一周每天的产量分别是:205,198,196,213,190,216,191
故产量最多的一天比产量最少的一天多生产216-190=26辆.
故答案为:26辆.
(3)一周生产电动车的总量数为:205+198+196+213+190+216+191=1409辆
故一周工人工资的总费用为:1409×60=84540元.
故答案为:84540元.


科目:初中数学 来源: 题型:
【题目】如图,Rt△ABC中,∠C=90°,AB=5,BC=4,点G为边BC的中点,点D从点C出发沿CA向点A运动,到点A停止,以GD为边作正方形DEFG,则点E运动的路程为_______.

查看答案和解析>>
科目:初中数学 来源: 题型:
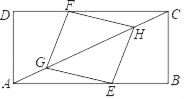
【题目】如图,矩形ABCD中,点E,F分别在边AB与CD上,点G、H在对角线AC上,AG=CH,BE=DF.
(1)求证:四边形EGFH是平行四边形;
(2)若EG=EH,AB=8,BC=4.求AE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在每个小正方形边长为1的方格纸内将△ABC经过一次平移后得到△A′B′C′,图中标出了点B的对应点B′.根据下列条件,利用格点和三角尺画图:
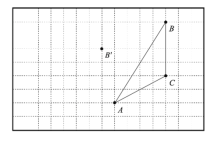
(1)补全△A′B′C′;
(2)请在AC边上找一点D,使得线段BD平分△ABC的面积,在图上作出线段BD;
(3)利用格点在图中画出AC边上的高线BE;
(4)求△ABD的面积_______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】设M(m,n)在反比例函数y=﹣ ![]() 上,其中m是分式方程
上,其中m是分式方程 ![]() ﹣1=
﹣1= ![]() 的根,将M点先向上平移4个单位,再向左平移1个单位,得到点N.若点M,N都在直线y=kx+b上,直线解析式为( )
的根,将M点先向上平移4个单位,再向左平移1个单位,得到点N.若点M,N都在直线y=kx+b上,直线解析式为( )
A.y=﹣ ![]() x﹣
x﹣ ![]()
B.y= ![]() x+
x+ ![]()
C.y=4x﹣5
D.y=﹣4x+5
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两车从A地开往B地,全程800km;所行的路程与时间的函数图像如图所示,下列问题:①乙车比甲车早出发2h;②甲车追上乙车时行驶了300km;③乙车的速度小于甲车速度;④甲车跑完全程比乙车跑完全程少用3h;以上正确的序号是_______.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】列方程(或方程组)解应用题:
(1)某服装店到厂家选购甲、乙两种服装,若购进甲种服装9件、乙种服装10件,需1810元;购进甲种服装11件乙种服装8件,需1790元,求甲乙两种服装每件价格相差多少元?
(2)某工厂现库存某种原料1200吨,用来生产A、B两种产品,每生产1吨A产品需这种原料2吨、生产费用1000元;每生产1吨B产品需这种原料2.5吨、生产费用900元,如果用来生产这两种产品的资金为53万元,那么A、B两种产品各生产多少吨才能使库存原料和资金恰好用完?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】你能比较![]() 与
与![]() 的大小吗?为了解决这个问题,先把问题一般化.即比较
的大小吗?为了解决这个问题,先把问题一般化.即比较![]() 与
与![]() 的大小(整数n≥1).然后,从分析n=1,n=2, n=3,……这些简单情形入手,从中发现规律,经过归纳、猜想,得出结论.
的大小(整数n≥1).然后,从分析n=1,n=2, n=3,……这些简单情形入手,从中发现规律,经过归纳、猜想,得出结论.
(1)通过计算,比较下列①到⑥各组中两个数的大小:
① ![]() ②
② ![]() ③
③![]()
④![]() ⑤
⑤![]() ⑥
⑥![]()
(2)从(1)小题的结果归纳,请猜想![]() 与
与![]() 的大小关系:
的大小关系:
(3)根据上面归纳猜想到的一般结论,可以得到:
![]() _______
_______ ![]() (填“>”、“=”或“<”).
(填“>”、“=”或“<”).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com