
 如图,△ABC为等边三角形,D,E两点分别在AB,AC边上,DB=AE,BE,CD相交于点F,BH⊥CD于点H,若EF=1,CD=9,求HF的长.
如图,△ABC为等边三角形,D,E两点分别在AB,AC边上,DB=AE,BE,CD相交于点F,BH⊥CD于点H,若EF=1,CD=9,求HF的长. 分析 只要证明△ABE≌△CBD,推出∠ABE=∠BCD,BE=CD=9,由EF=1,推出BF=BE-EF=8,在Rt△FBH中 只要证明∠FBH=30°,即可解决问题.
解答 解:∵△ABC是等边三角形,
∴AB=BC,∠A=∠ABC=60°,
在△ABE和△BCD中,
$\left\{\begin{array}{l}{AB=BC}\\{∠A=∠DBC}\\{AE=BD}\end{array}\right.$,
∴△ABE≌△CBD,
∴∠ABE=∠BCD,BE=CD=9,
∵EF=1,
∴BF=BE-EF=8,
∵∠BFH=∠BCD+∠CBE=∠ABE+∠CBE=∠ABC=60°,
∵BH⊥CD,
∴∠BHF=90°,∠FBH=30°,
∴HF=$\frac{1}{2}$BF=4.
点评 本题考查等边三角形的性质、全等三角形的判定和性质,直角三角形30度角性质等知识,解题的关键是正确寻找全等三角形解决问题,本题的突破点是证明∠FBH=30°,属于中考常考题型.


科目:初中数学 来源: 题型:选择题
 如图,在△ABC中,AB=AC=8,BC=12,分别以AB、AC为直径作半圆,则图中阴影部分的面积是( )
如图,在△ABC中,AB=AC=8,BC=12,分别以AB、AC为直径作半圆,则图中阴影部分的面积是( )| A. | 12π-16$\sqrt{7}$ | B. | 16π-18$\sqrt{7}$ | C. | 16π-24$\sqrt{7}$ | D. | 16π-12$\sqrt{7}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 ,剩下的工程由乙队单独做,也正好如期完工.某同学设规定的工期为x天,根据题意列出了方程:$\frac{4}{x}+\frac{x}{x+5}=1$,则方案③中被墨水污染的部分应该是( )
,剩下的工程由乙队单独做,也正好如期完工.某同学设规定的工期为x天,根据题意列出了方程:$\frac{4}{x}+\frac{x}{x+5}=1$,则方案③中被墨水污染的部分应该是( )| A. | 甲乙合作了4天 | B. | 甲先做了4天 | ||
| C. | 甲先做了工程的$\frac{1}{4}$ | D. | 甲乙合作了工程的$\frac{1}{4}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
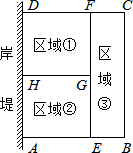 为了节省材料,某水产养殖户利用水库的岸堤(岸堤足够长)为一边,用总长为80米的围网在水库中围成了如图所示的①②③三块矩形区域,而且这三块矩形区域的面积相等.设BC的长度为x米,矩形区域ABCD的面积为y米2.
为了节省材料,某水产养殖户利用水库的岸堤(岸堤足够长)为一边,用总长为80米的围网在水库中围成了如图所示的①②③三块矩形区域,而且这三块矩形区域的面积相等.设BC的长度为x米,矩形区域ABCD的面积为y米2.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com