
 如图,在△ABC中,AB=AC=8,BC=12,分别以AB、AC为直径作半圆,则图中阴影部分的面积是( )
如图,在△ABC中,AB=AC=8,BC=12,分别以AB、AC为直径作半圆,则图中阴影部分的面积是( )| A. | 12π-16$\sqrt{7}$ | B. | 16π-18$\sqrt{7}$ | C. | 16π-24$\sqrt{7}$ | D. | 16π-12$\sqrt{7}$ |
分析 根据AB=AC,AB=8,BC=12,分别以AB、AC为直径作半圆,得出BD=DC,以及图中阴影部分的面积是:圆的面积-S△ABC分别求出即可.
解答 解:连接AD,
∵AB=AC,AB=8,BC=12,以AB、AC为直径作半圆,
∴∠ADB=∠ADC=90°,即AD⊥BC,
∴BD=CD=6,
∴AD⊥BC,
∴AD=$\sqrt{A{C}^{2}-C{D}^{2}}=\sqrt{64-36}=2\sqrt{7}$,
∴S△ABC=$\frac{1}{2}$×AD×BC=$\frac{1}{2}$×2$\sqrt{7}$×12=12$\sqrt{7}$,
∵图中阴影部分的面积是:圆的面积-S△ABC=π×42-12$\sqrt{7}$=16π-12$\sqrt{7}$.
故选D
点评 此题主要考查了勾股定理以及等腰三角形的性质,根据已知得出AD的长以及圆的面积减去△ABC的面积是解题关键.


 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案 名题训练系列答案
名题训练系列答案 期末集结号系列答案
期末集结号系列答案科目:初中数学 来源: 题型:解答题
 如图,河岸边有座塔AB,小敏在河对岸C处测得塔顶A的仰角为30°,向塔前进20米到达D处,又测得塔顶A的仰角为45°,请根据上述数据计算水塔的高.
如图,河岸边有座塔AB,小敏在河对岸C处测得塔顶A的仰角为30°,向塔前进20米到达D处,又测得塔顶A的仰角为45°,请根据上述数据计算水塔的高.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,点F、B、E、C在同一直线上,并且BF=CE,∠ABC=∠DEF,能否由上面的已知条件证明AC∥DF?如果能,请给出证明;如果不能,请从下列三个条件中选择一个合适的条件,添加到已知条件中,使AC∥DF,并给出证明.
如图,点F、B、E、C在同一直线上,并且BF=CE,∠ABC=∠DEF,能否由上面的已知条件证明AC∥DF?如果能,请给出证明;如果不能,请从下列三个条件中选择一个合适的条件,添加到已知条件中,使AC∥DF,并给出证明.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,△ABC为等边三角形,D,E两点分别在AB,AC边上,DB=AE,BE,CD相交于点F,BH⊥CD于点H,若EF=1,CD=9,求HF的长.
如图,△ABC为等边三角形,D,E两点分别在AB,AC边上,DB=AE,BE,CD相交于点F,BH⊥CD于点H,若EF=1,CD=9,求HF的长.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
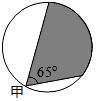 如图,是一个圆形展厅,为了监控整个展厅,在其圆形边缘上安装了甲、乙两台监视器,若甲监视器的监控角度为65°,则乙监控器的监控角度至少为( )
如图,是一个圆形展厅,为了监控整个展厅,在其圆形边缘上安装了甲、乙两台监视器,若甲监视器的监控角度为65°,则乙监控器的监控角度至少为( )| A. | 25° | B. | 65° | C. | 115° | D. | 130° |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | a2-(2a-1)=a2-2a-1 | B. | a2+(-2a-3)=a2-2a+3 | ||
| C. | -(a+b)+(c-d)=-a-b-c+d | D. | 3a-[5b-(2c-1)]=3a-5b+2c-1 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com