
 ,剩下的工程由乙队单独做,也正好如期完工.某同学设规定的工期为x天,根据题意列出了方程:$\frac{4}{x}+\frac{x}{x+5}=1$,则方案③中被墨水污染的部分应该是( )
,剩下的工程由乙队单独做,也正好如期完工.某同学设规定的工期为x天,根据题意列出了方程:$\frac{4}{x}+\frac{x}{x+5}=1$,则方案③中被墨水污染的部分应该是( )| A. | 甲乙合作了4天 | B. | 甲先做了4天 | ||
| C. | 甲先做了工程的$\frac{1}{4}$ | D. | 甲乙合作了工程的$\frac{1}{4}$ |
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,点F、B、E、C在同一直线上,并且BF=CE,∠ABC=∠DEF,能否由上面的已知条件证明AC∥DF?如果能,请给出证明;如果不能,请从下列三个条件中选择一个合适的条件,添加到已知条件中,使AC∥DF,并给出证明.
如图,点F、B、E、C在同一直线上,并且BF=CE,∠ABC=∠DEF,能否由上面的已知条件证明AC∥DF?如果能,请给出证明;如果不能,请从下列三个条件中选择一个合适的条件,添加到已知条件中,使AC∥DF,并给出证明.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,△ABC为等边三角形,D,E两点分别在AB,AC边上,DB=AE,BE,CD相交于点F,BH⊥CD于点H,若EF=1,CD=9,求HF的长.
如图,△ABC为等边三角形,D,E两点分别在AB,AC边上,DB=AE,BE,CD相交于点F,BH⊥CD于点H,若EF=1,CD=9,求HF的长.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 40m-10=43m-1 | B. | 40m+10=43m+1 | C. | 43(n-10)=40(n-1) | D. | $\frac{n-10}{40}$=$\frac{n-1}{43}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
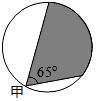 如图,是一个圆形展厅,为了监控整个展厅,在其圆形边缘上安装了甲、乙两台监视器,若甲监视器的监控角度为65°,则乙监控器的监控角度至少为( )
如图,是一个圆形展厅,为了监控整个展厅,在其圆形边缘上安装了甲、乙两台监视器,若甲监视器的监控角度为65°,则乙监控器的监控角度至少为( )| A. | 25° | B. | 65° | C. | 115° | D. | 130° |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com