
科目:初中数学 来源: 题型:选择题
| A. | 两直线平行,同旁内角相等 | |
| B. | 三角形的一个外角大于任何一个内角 | |
| C. | 三角形三条边的垂直平分线相交于一点,且这一点到三边的距离相等 | |
| D. | 两角分别相等且其中一组等角的对边相等的两个三角形全等 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 等腰三角形 | B. | 等边三角形 | C. | 锐角三角形 | D. | 直角三角形 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
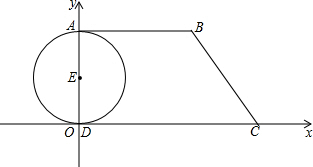 如图,在平面直角坐标系中,直角梯形ABCD的直角顶点D与原点重合,另一直角顶点A在y轴的正半轴上,点B、C的坐标分别为B(12,8)、C(14,0),AD为⊙E的直径.点M、N分别从A、C两点同时出发做匀速运动,其中点M沿AB向终点B运动,速度为每秒1个单位;点N沿CD向终点D运动,速度为每秒3个单位.当这两点中有一点到达自己的终点时,另一点也停止运动.
如图,在平面直角坐标系中,直角梯形ABCD的直角顶点D与原点重合,另一直角顶点A在y轴的正半轴上,点B、C的坐标分别为B(12,8)、C(14,0),AD为⊙E的直径.点M、N分别从A、C两点同时出发做匀速运动,其中点M沿AB向终点B运动,速度为每秒1个单位;点N沿CD向终点D运动,速度为每秒3个单位.当这两点中有一点到达自己的终点时,另一点也停止运动.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com